
科目: 来源: 题型:
【题目】问题提出
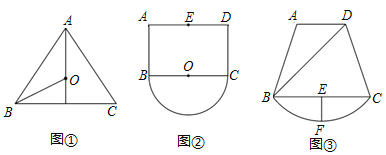
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
查看答案和解析>>
科目: 来源: 题型:
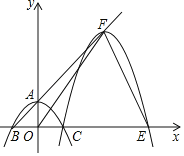
【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4,现将抛物线沿BA方向平移,平移后的抛物线过点C时,与x轴的另一交点为E,其顶点为F.
(1)求a、c的值;
(2)连接OF,试判断△OEF是否为等腰三角形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
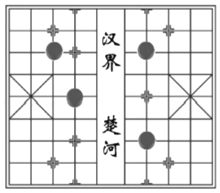
【题目】象棋是棋类益智游戏,中国象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.李凯和张萌利用象棋棋盘和棋子做游戏.李凯将四枚棋子反面朝上放在棋盘上,其中有两个“兵”、一个“马”、一个“士”,张萌随机从这四枚棋子中摸一枚棋子,记下正汉字,然后再从剩下的三枚棋子中随机摸一枚.
(1)求张萌第一次摸到的棋子正面上的汉字是“兵”的概率;
(2)游戏规定:若张萌两次摸到的棋子中有“士”,则张萌胜;否则,李凯胜.请你用树状图或列表法求李凯胜的概率.
查看答案和解析>>
科目: 来源: 题型:
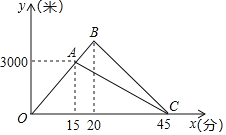
【题目】张琪和爸爸到曲江池遗址公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示
(1)求爸爸返问时离家的路程y2(米)与运动时间x(分)之间的函数关系式;
(2)张琪开始返回时与爸爸相距多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48B.36C.24D.18
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 和抛物线
和抛物线![]() (
(![]() 为正整数).
为正整数).
(1)抛物线![]() 与
与![]() 轴的交点______,顶点坐标______;
轴的交点______,顶点坐标______;
(2)当![]() 时,请解答下列问题.
时,请解答下列问题.
①直接写出![]() 与
与![]() 轴的交点______,顶点坐标______,请写出抛物线
轴的交点______,顶点坐标______,请写出抛物线![]() ,
,![]() 的一条相同的图象性质______;
的一条相同的图象性质______;
②当直线![]() 与
与![]() ,
,![]() 相交共有4个交点时,求
相交共有4个交点时,求![]() 的取值范围.
的取值范围.
(3)若直线![]() (
(![]() )与抛物线
)与抛物线![]() ,抛物线
,抛物线![]() (
(![]() 为正整数)共有4个交点,从左至右依次标记为点
为正整数)共有4个交点,从左至右依次标记为点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ,当
,当![]() 时,求出
时,求出![]() ,
,![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目: 来源: 题型:
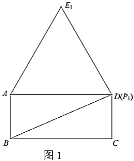
【题目】已知:矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,连接
上的一个动点,连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作等边
的右侧作等边![]() .
.
(1)①如图1,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,则点
,则点![]() 到
到![]() 的距离是________;
的距离是________;
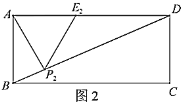
②如图2,当点![]() 运动到点
运动到点![]() 落在
落在![]() 上时,记等边
上时,记等边![]() 为等边
为等边![]() .则等边
.则等边![]() 的边长
的边长![]() 是________;
是________;
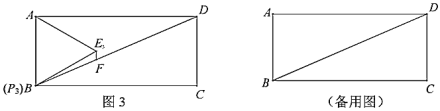
(2)如图3,当点![]() 运动到与点
运动到与点![]() 重合时,记等边
重合时,记等边![]() 为等边
为等边![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长;
的长;
(3)①在上述变化过程中的点![]() ,
,![]() ,
,![]() 是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
是否在同一直线上?请建立平面直角坐标系加以判断,并说明理由.
②点![]() 的位置随着动点
的位置随着动点![]() 在线段
在线段![]() 上的位置变化而变化,猜想关于所有点
上的位置变化而变化,猜想关于所有点![]() 的位置的一个数学结论,试用一句话表述:______.
的位置的一个数学结论,试用一句话表述:______.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年某水果加工公司分两次采购了一批桃子,第一次费用为25万元,第二次费用为30万元.已知第一次采购时每吨桃子的价格比去年的平均价格上涨了0.1万元,第二次采购时每吨桃子的价格比去年的平均价格下降了0.1万元,第二次采购的数量是第一次采购数量的2倍.
(1)试问去年每吨桃子的平均价格是多少万元?两次采购的总数量是多少吨?
(2)该公司可将桃子加工成桃脯或桃汁,每天只能加工其中一种.若单独加工成桃脯,每天可加工3吨桃子,每吨可获利0.7万元;若单独加工成桃汁,每天可加工9吨桃子,每吨可获利0.2万元.为出口需要,所有采购的桃子必须在30天内加工完毕.
①根据该公司的生产能力,加工桃脯的时间不能超过多少天?
②在这次加工生产过程中,应将多少吨桃子加工成桃脯才能获取最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com