
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线ABy=kx﹣1分别交x轴、y轴于点A、B,直线CDy=x+2分别交x轴、y轴于点D、C,且直线AB、CD交于点E,E的横坐标为﹣6.
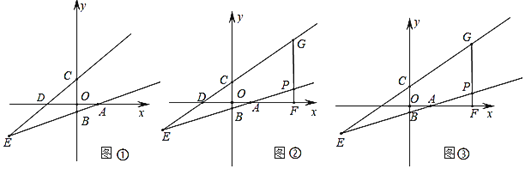
(1)如图①,求直线AB的解析式;
(2)如图②,点P为直线BA第一象限上一点,过P作y轴的平行线交直线CD于G,交x轴于F,在线段PG取点N,在线段AF上取点Q,使GN=QF,在DG上取点M,连接MN、QN,若∠GMN=∠QNF,求![]() 的值;
的值;
(3)在(2)的条件下,点E关于x轴对称点为T,连接MP、TQ,若MP∥TQ,且GN:NP=4:3,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,半径为1的⊙O与x轴正半轴和y轴正半轴分别交于A,B两点,直线l:y=kx+2(k<0)与x轴和y轴分别交于P,M两点.
(1)当直线与⊙O相切时,求出点M的坐标和点P的坐标;
(2)如图2,当点P在线段OA上时,直线1与⊙O交于E,F两点(点E在点F的上方)过点F作FC∥x轴,与⊙O交于另一点C,连结EC交y轴于点D.
①如图3,若点P与点A重合时,求OD的长并写出解答过程;
②如图2,若点P与点A不重合时,OD的长是否发生变化,若不发生变化,请求出OD的长并写出解答过程;若发生变化,请说明理由.
(3)如图4,在(2)的基础上,连结BF,将线段BF绕点B逆时针旋转90°到BQ,若点Q在CE的延长线时,请用等式直接表示线段FC,FQ之间的数量关系.

查看答案和解析>>
科目: 来源: 题型:
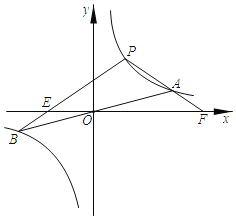
【题目】如图,双曲线y1=![]() 与直线y2=
与直线y2=![]() 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=![]() 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.
(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=![]() 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了促进各科均衡发展,学校准备在九年级下期开设四科补短班,分别是英语、数学、物理和化学.为提前了解同学们最想参加的科目,学校在开学前采用随机抽样方式进行了调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息完成以下问题.
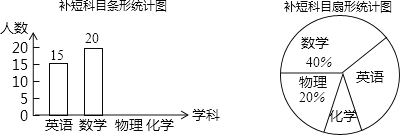
(1)扇形统计图中,“英语”所在扇形的圆心角度数是 ,并补全条形统计图;
(2)在被调查的学生中,选择化学的有2名女同学,其余为男同学,现要从中随机抽取2名同学参加学科座谈会,请用画树状图或列表的方法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某专卖店有A、B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.A、B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,请问A、B两种商品打折前各多少钱?打了多少折?
查看答案和解析>>
科目: 来源: 题型:
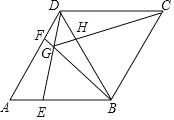
【题目】如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,则BG=6GF;![]() .其中正确的结论有_____(填序号).
.其中正确的结论有_____(填序号).
查看答案和解析>>
科目: 来源: 题型:
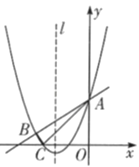
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
x+3分别相交于A,B两点,且此抛物线与x轴的一个交点为C,连接AC,BC.已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MC|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
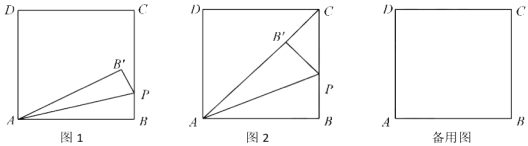
【题目】如图1,在矩形![]() 中,BC=3,动点
中,BC=3,动点![]() 从
从![]() 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]()
(1)若![]()
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com