
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
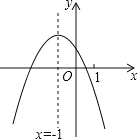
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】给定一个函数,如果这个函数的图象上存在一个点,它的横、纵坐标相等,那么这个点叫做该函数的不变点.
(1)一次函数![]() 的不变点的坐标为______.
的不变点的坐标为______.
(2)二次函数![]() 的两个不变点分别为点
的两个不变点分别为点![]() (
(![]() 在
在![]() 的左侧),将点
的左侧),将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)已知二次函数![]() 的两个不变点的坐标为
的两个不变点的坐标为![]() .
.
①求![]() 的值;
的值;
②如图,设抛物线![]() 与线段
与线段![]() 围成的封闭图形记作
围成的封闭图形记作![]() .点
.点![]() 为一次函数
为一次函数![]() 的不变点,以线段
的不变点,以线段![]() 为边向下作正方形
为边向下作正方形![]() .当
.当![]() 两点中只有一个点在封闭图形
两点中只有一个点在封闭图形![]() 的内部(不包含边界)时,求出
的内部(不包含边界)时,求出![]() 的取值范围.
的取值范围.
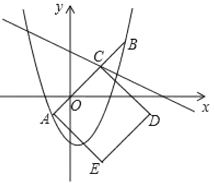
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:数学课上,老师出示了这样一个问题:
如图1,在等边![]() 中,点
中,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 延长线于
延长线于![]() 点,且
点,且![]() ,探究线段
,探究线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
某学习小组的同学经过思考,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 存在某种数量关系”;
存在某种数量关系”;
小强:“通过观察和度量,发现图1中有一条线段与![]() 相等”;
相等”;
小伟:“通过构造三角形,证明三角形全等,进而可以得到线段![]() 之间的数量关系”.
之间的数量关系”.
……
老师:“保留原题条件,再过点![]() 作
作![]() 交
交![]() 于
于![]() 与
与![]() 相交于点
相交于点![]() (如图2)如果给出
(如图2)如果给出![]() 的值,那么可以求出
的值,那么可以求出![]() 的值”.
的值”.
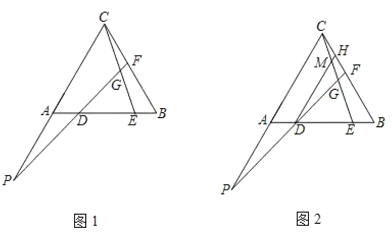
请回答:
(1)在图1中找出![]() 与
与![]() 数量关系,并证明;
数量关系,并证明;
(2)在图1中找出与线段![]() 相等的线段,并证明;
相等的线段,并证明;
(3)探究线段![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(4)若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以
出发,以![]() 的速度分别沿
的速度分别沿![]() 、
、![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() .过点
.过点![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称.
对称.
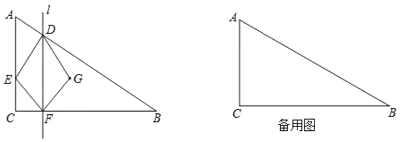
(1)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 的平分线上;
的平分线上;
(2)当![]() _____
_____![]() 时,点
时,点![]() 在
在![]() 边上;
边上;
(3)设![]() 与
与![]() 重合部分的面积为
重合部分的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写
之间的函数关系式,并写![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解![]() 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
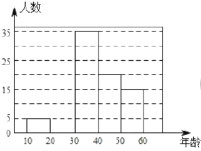
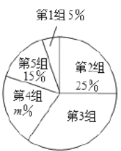
(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有![]() 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=![]() x2+bx+3的对称轴为直线x=
x2+bx+3的对称轴为直线x=![]() 1.若关于x的一元二次方程
1.若关于x的一元二次方程![]() x2+bx+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
x2+bx+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
A.![]() 12<t≤3B.
12<t≤3B.![]() 12<t<4C.
12<t<4C.![]() 12<t≤4D.
12<t≤4D.![]() 12<t<3
12<t<3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com