
科目: 来源: 题型:
【题目】上海市为了增强居民的节水意识,避免水资源的浪费,全面实施居民“阶梯水价”.当累计水量达到年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和价格见下表.
分档 | 户年用水量 (立方米) | 自来水价格 (元/立方米) | 污水处理费 (元/立方米) |
第一阶梯 | 0-220(含220) | 1.92 | 1.70 |
第二阶梯 | 220-300(含300) | 3.30 | 1.70 |
第三阶梯 | 300以上 | 4.30 | 1.70 |
注:1.应缴纳水费 = 自来水费总额 + 污水处理费总额 2.应缴纳污水处理费总额 = 用水量×污水处理费× 0.9 | |||
仔细阅读上述材料,请解答下面的问题,并把答案写在答题纸上:
(1)小静家2019年上半年共计用水量100立方米,应缴纳水费 元;
(2)小静家全年缴纳的水费共计1000.5元,那么2019年全年用水量为 立方米;
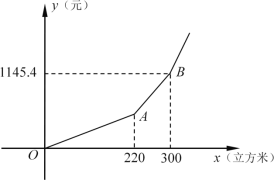
(3)如图所示是上海市“阶梯水价”y与用水量x的函数关系,那么第二阶梯(线段AB)的函数解析式为 ,定义域 .
查看答案和解析>>
科目: 来源: 题型:
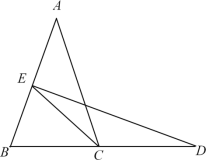
【题目】已知:如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
(1)求CD的长;
(2)求点C到ED的距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题中正确的个数是( )
①过三点可以确定一个圆
②直角三角形的两条直角边长分别是5和12,那么它的外接圆半径为6.5
③如果两个半径为2厘米和3厘米的圆相切,那么圆心距为5厘米
④三角形的重心到三角形三边的距离相等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于任意两点
中,对于任意两点![]() ,
,![]() ,如果
,如果![]() ,则称
,则称![]() 与
与![]() 互为“
互为“![]() 距点”.例如:点
距点”.例如:点![]() ,点
,点![]() ,由
,由![]() ,可得点
,可得点![]() 与
与![]() 互为“
互为“![]() 距点”.
距点”.
(1)在点![]() ,
,![]() ,
,![]() 中,原点
中,原点![]() 的“
的“![]() 距点”是_____(填字母);
距点”是_____(填字母);
(2)已知点![]() ,点
,点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
①当![]() 时,直线
时,直线![]() 上点
上点![]() 的“
的“![]() 距点”的坐标为_____;
距点”的坐标为_____;
②若直线![]() 上存在点
上存在点![]() 的“
的“![]() 点”,求
点”,求![]() 的取值范围.
的取值范围.
(3)已知点![]() ,
,![]() ,
,![]() ,
,![]() 的半径为
的半径为![]() ,若在线段
,若在线段![]() 上存在点
上存在点![]() ,在
,在![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 与点
与点![]() 互为“
互为“![]() 距点”,直接写出
距点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月17日世界人工智能大会在上海召开,人工智能的变革力在教育、制造等领域加速落地. 在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一部分.
排名 | 代表队 | 场次 (场) | 胜 (场) | 平 (场) | 负 (场) | 净胜球 (个) | 进球 (个) | 失球 (个) | 积分 (分) |
1 | A | 6 | 1 | 6 | 12 | 6 | 22 | ||
2 | B | 6 | 3 | 2 | 1 | 0 | 6 | 6 | 19 |
3 | C | 6 | 3 | 1 | 2 | 2 | 9 | 7 | 17 |
4 | D | 6 | 0 | 0 | 6 | m | 5 | 13 | 0 |
(说明:积分=胜场积分+平场积分+负场积分)
(1)D代表队的净胜球数m= ;
(2)本次决赛中,胜一场积 分,平一场积 分,负一场积 分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.
请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
科目: 来源: 题型:
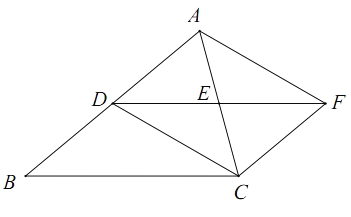
【题目】如图,在△ABC中,D为AB中点,过点D作DF//BC交AC于点E,且DE=EF,连接AF,CF,CD.
(1)求证:四边形ADCF为平行四边形;
(2)若∠ACD=45°,∠EDC=30°,BC=4,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温(![]() )与时间(小时)之间的关系如图1所示.
)与时间(小时)之间的关系如图1所示.

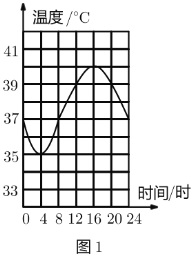
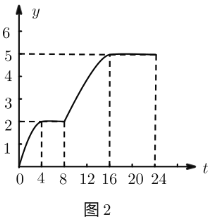
小清同学根据图1绘制了图2,则图2中的变量有可能表示的是( ).
A.骆驼在![]() 时刻的体温与0时体温的绝对差(即差的绝对值)
时刻的体温与0时体温的绝对差(即差的绝对值)
B.骆驼从0时到![]() 时刻之间的最高体温与当日最低体温的差
时刻之间的最高体温与当日最低体温的差
C.骆驼在![]() 时刻的体温与当日平均体温的绝对差
时刻的体温与当日平均体温的绝对差
D.骆驼从0时到![]() 时刻之间的体温最大值与最小值的差
时刻之间的体温最大值与最小值的差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com