
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴交于另一点
轴交于另一点![]() .
.
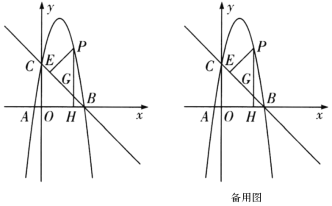
(1)求抛物线的解析式;
(2)点![]() 为第一象限内抛物线上一动点,过点
为第一象限内抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() 的长度为
的长度为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出当
,并求出当![]() 取得最大值时,点
取得最大值时,点![]() 的坐标.
的坐标.
②在①的条件下,当直线![]() 到直线
到直线![]() 的距离等于
的距离等于![]() 时,请直接写出符合要求的直线
时,请直接写出符合要求的直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目: 来源: 题型:
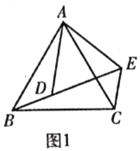
【题目】(1)(问题发现)如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上.填空:①线段
在同一条直线上.填空:①线段![]() ,
,![]() 之间的数量关系为______;②
之间的数量关系为______;②![]() _____°.
_____°.
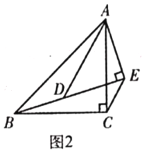
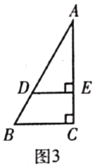
(2)(类比探究)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,请判断线段
在同一条直线上,请判断线段![]() ,
,![]() 之间的数量关系及
之间的数量关系及![]() 的度数,并给出证明.
的度数,并给出证明.
(3)(解决问题)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() 于点
于点![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 所在直线经过点
所在直线经过点![]() 时,
时,![]() 的长是多少?(直接写出答案)
的长是多少?(直接写出答案)
查看答案和解析>>
科目: 来源: 题型:
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 | <> |
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
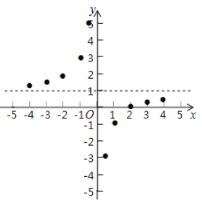
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某社会团体准备购进甲、乙两种防护服捐给一线抗疫人员,经了解,购进5件甲种防护服和4件乙种防护服需要2万元,购进10件甲种防护服和3件乙种防护服需要3万元.
(1)甲种防护服和乙种防护服每件各多少元?
(2)实际购买时,发现厂家有两种优惠方案,方案一:购买甲种防护服超过20件时,超过的部分按原价的8折付款,乙种防护服没有优惠;方案二:两种防护服都按原价的9折付款,该社会团体决定购买![]()
![]() 件甲种防护服和30件乙种防护服.
件甲种防护服和30件乙种防护服.
①求两种方案的费用![]() 与件数
与件数![]() 的函数解析式;
的函数解析式;
②请你帮该社会团体决定选择哪种方案更合算.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”的号召,某校开展了志愿者服务活动,活动项目有“防疫宜宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”五项,活动期间,随机抽取了部分学生对志思者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如下不完整的条形统计图和扇形统计图.
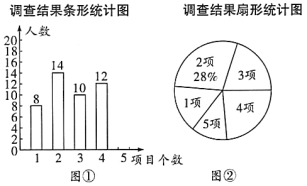
根据以上统计图解答下列问题:
(1)本次随机抽取的学生共有______名;
(2)补全条形统计图;
(3)若该校有3000名学生,请估计参与了4项活动的学生人数;
(4)在所调查的学生中随机选取一人谈活动心得,求选中参与了5项活动的学生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过A(﹣1,0),B两点,且与y轴交于点C(0,3),抛物线与直线y=﹣x﹣1交于A,E两点.
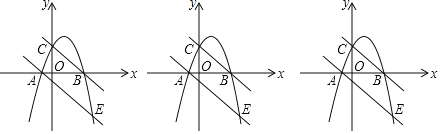
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点Q,使得△AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.
(3)P点在x轴上且位于点B的左侧,若以P,B,C为顶点的三角形与△ABE相似,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
(1)求证:△DAF≌△DCE.
(2)求证:DE是⊙O的切线.
(3)若BF=2,DH=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
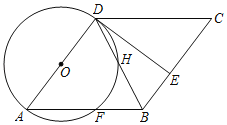
查看答案和解析>>
科目: 来源: 题型:
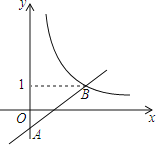
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数![]() (x>0)的图象相交于点B(t,1).
(x>0)的图象相交于点B(t,1).
(1)求点B的坐标及一次函数的解析式;
(2)点P的坐标为(m,m)(m>0),过P作PE∥x轴,交直线AB于点E,作PF∥y轴,交函数![]() (x>0)的图象于点F.
(x>0)的图象于点F.
①若m=2,比较线段PE,PF的大小;
②直接写出使PE≤PF的m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明家所在居民楼的对面有一座大厦AB,高为74米,为测量居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.
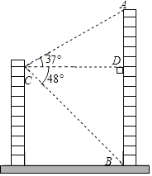
(1)求∠ACB的度数;
(2)求小明家所在居民楼与大厦之间的距离.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,cos48°≈
,cos48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com