
科目: 来源: 题型:
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
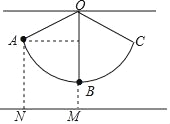
【答案】15cm
【解析】
试题设细线OB的长度为xcm,作AD⊥OB于D,证出四边形ANMD是矩形,得出AN=DM=14cm,求出OD=x-9,在Rt△AOD中,由三角函数得出方程,解方程即可.
试题解析:设细线OB的长度为xcm,作AD⊥OB于D,如图所示:
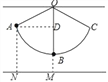
∴∠ADM=90°,
∵∠ANM=∠DMN=90°,
∴四边形ANMD是矩形,
∴AN=DM=14cm,
∴DB=14﹣5=9cm,
∴OD=x﹣9,
在Rt△AOD中,cos∠AOD=![]() ,
,
∴cos66°=![]() =0.40,
=0.40,
解得:x=15,
∴OB=15cm.
【题型】解答题
【结束】
20
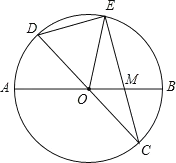
【题目】已知:如图,在半径为![]() 的
的![]() 中,
中,![]() 、
、![]() 是两条直径,
是两条直径,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,且
,且![]() ,连接
,连接![]() 。
。![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 出发沿
出发沿![]() 方向在运动速度为3个单位/秒,点
方向在运动速度为3个单位/秒,点![]() 从
从![]() 出发向点
出发向点![]() 运动,速度为1个单位/秒,
运动,速度为1个单位/秒,![]() 、
、![]() 同时出发,点
同时出发,点![]() 到点
到点![]() 时两点同时停止运动.
时两点同时停止运动.
(1)点![]() 在线段
在线段![]() 上运动,过
上运动,过![]() 作
作![]() 交边
交边![]() 于
于![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(2)运动![]() 秒后,
秒后,![]() ,求此时
,求此时![]() 的值;
的值;
(3)![]() ________时,
________时,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
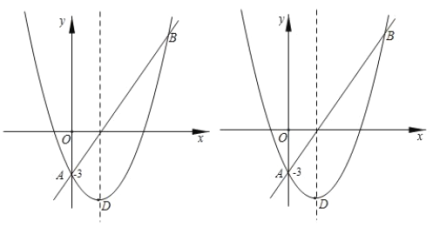
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长六寸,问径几何?”用现代的数学语言表述是:“CD为![]() 的直径,弦
的直径,弦![]() ,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
,垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意得CD的长为( )
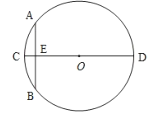
A.12寸B.13寸C.24寸D.26寸
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线yx m交 y轴的正半轴于点A,交x轴的正半轴于点B,过点A的直线AF交x轴的负半轴于点F,∠AFO=45°.
(1)求∠FAB的度数;
(2)点 P是线段OB上一点,过点P作 PQ⊥OB交直线 FA于点Q,连接 BQ,取 BQ的中点C,连接AP、AC、CP,过点C作 CR⊥AP于点R,设 BQ的长为d,CR的长为h,求d与 h的函数关系式(不要求写出自变量h的取值范围);
(3)在(2)的条件下,过点 C 作 CE⊥OB于点E,CE交 AB于点D,连接 AE,∠AEC=2∠DAP,EP=2,作线段 CD 关于直线AB的对称线段DS,求直线PS与直线 AF的交点K的坐标.

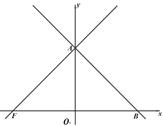
查看答案和解析>>
科目: 来源: 题型:
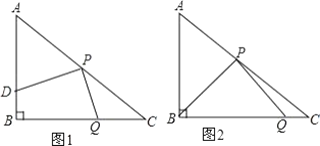
【题目】已知:矩形ABCD内接于⊙O,连接 BD,点E在⊙O上,连接 BE交 AD于点F,∠BDC+45°=∠BFD,连接ED.
(1)如图 1,求证:∠EBD=∠EDB;
(2)如图2,点G是 AB上一点,过点G作 AB的垂线分别交BE和 BD于点H和点K,若HK=BG+AF,求证:AB=KG;
(3)如图 3,在(2)的条件下,⊙O上有一点N,连接 CN分别交BD和 AD于![]() 点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
点 M和点 P,连接 OP,∠APO=∠CPO,若 MD=8,MC= 3,求线段 GB的长.
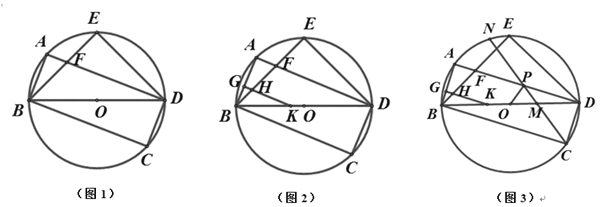
查看答案和解析>>
科目: 来源: 题型:
【题目】为美化小区环境,物业计划安排甲、乙两个工程队完成小区绿化工作.已知甲工程队每天绿化面积是乙工程队每天绿化面积的2倍,甲工程队单独完成600m2的绿化面积比乙工程队单独完成600m2的绿化面积少用2天.
(1)求甲、乙两工程队每天绿化的面积分别是多少m2;
(2)小区需要绿化的面积为9600m2,物业需付给甲工程队每天绿化费为0.3万元,付给乙工程队每天绿化费为 0.2万元,若要使这次的绿化总费用不超过10万元,则至少应安排甲工程队工作多少天?
查看答案和解析>>
科目: 来源: 题型:
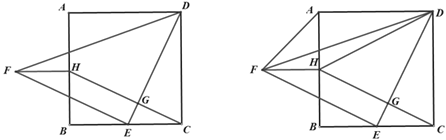
【题目】已知:在正方形ABCD中,点E在 BC边上,连接 DE,以DE为直角边作等腰直角三角形EDF(∠DEF=90°),过点C作 DE的垂线,垂足为G,交AB于点H,连接 FH.
(1)如图 1,求证:四边形FECH为平行四边形
(2)如图 2,连接 DH和 AF,点 E 为 BC 中点,在不添加任何辅助线与字母的情况下,请直接写出与平行四边形FECH面积相等的所有三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生对中国民族乐器的喜爱情况,某校在全校范围内随机抽取了部分学生进行问卷调查,要求学生在“古筝、二胡、竹笛、扬琴、琵琶”五个选项中,选取自己喜爱的一种乐器(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的两幅不完整的统计图.请你根据图中提供的信息回答下列问题:
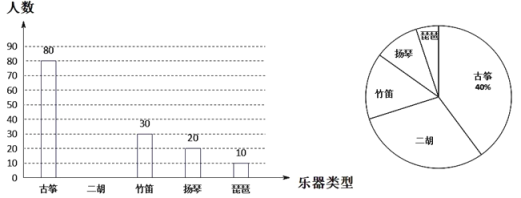
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若该校共有2020名学生,请你估计该校喜爱“竹笛”的学生有多少名.
查看答案和解析>>
科目: 来源: 题型:
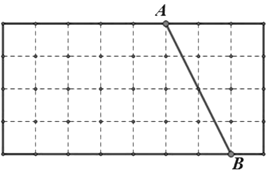
【题目】如图,方格纸中的每个小正方形的边长均为1,线段 AB的两个端点均在小正方形的顶点上.
(1)在图中画出以AB为直角边的Rt△ABC,点C在小正方形的顶点上,且Rt△ABC的面积为5;
(2)在(1)的条件下,画出△BCD,点D在小正方形的顶点上,且tan∠CDB![]() ,连接AD,请直接写出线段AD的长.
,连接AD,请直接写出线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com