
科目: 来源: 题型:
【题目】把函数![]() 的图象绕点
的图象绕点![]() 旋转
旋转![]() ,得到新函数
,得到新函数![]() 的图象,我们称
的图象,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图象的对称轴与
的图象的对称轴与![]() 轴交点坐标为
轴交点坐标为![]() .
.
(1)填空:![]() 的值为 (用含
的值为 (用含![]() 的代数式表示)
的代数式表示)
(2)若![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的解析式;
的解析式;
(3)当![]() 时,
时,![]() 的图象与
的图象与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧).与
的右侧).与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 原点
原点![]() 逆时针旋转
逆时针旋转![]() ,得到它的对应线段
,得到它的对应线段![]() ,若线
,若线![]() 与
与![]() 的图象有公共点,结合函数图象,求
的图象有公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
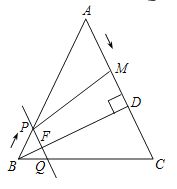
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时直线
;同时直线![]() 由点
由点![]() 出发沿
出发沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,运动过程中始终保持
,运动过程中始终保持![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)![]() ___________,
___________,![]() __________,
__________,![]() _____________;(用含
_____________;(用含![]() 的式子表示)
的式子表示)
(2)当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值;
的值;
(3)当点![]() 在线段
在线段![]() 的垂直平分线上时,求
的垂直平分线上时,求![]() 的值;
的值;
(4)是否存在时刻![]() ,使以
,使以![]() 为直径的圆与
为直径的圆与![]() 的边相切?若存在,直接写出
的边相切?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
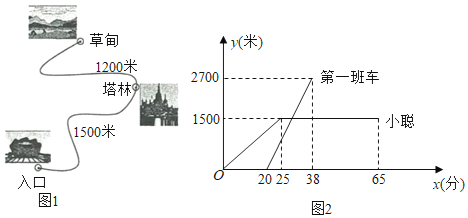
(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目: 来源: 题型:
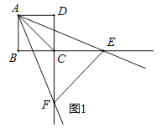
【题目】已知正方形![]() 的边长为4,一个以点
的边长为4,一个以点![]() 为顶点的
为顶点的![]() 角绕点
角绕点![]() 旋转,角的两边分别与边
旋转,角的两边分别与边![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,设
,设![]() .
.
(1)如图1,当![]() 被对角线
被对角线![]() 平分时,求
平分时,求![]() 的值;
的值;
(2)求证:![]() 与
与![]() 相似;
相似;
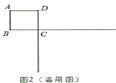
(3)当![]() 的外心在其边上时,求
的外心在其边上时,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级成绩频数分布直方图:

b.七年级成绩在![]() 这一组的是:70 72 74 75 76 76 77 77 77 78 79
这一组的是:70 72 74 75 76 76 77 77 77 78 79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | m |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在80分以上(含80分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;
(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.
查看答案和解析>>
科目: 来源: 题型:
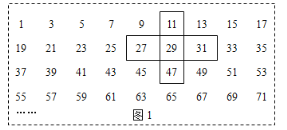
【题目】图1为奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为![]() ,其它四个数分别记为
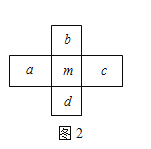
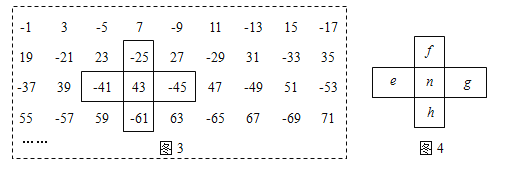
,其它四个数分别记为![]() (如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为
(如图2);图3为按某一规律排成的另一个数表,用十字框任意框出5个数,记框内中间这个数为![]() ,其它四个数记为
,其它四个数记为![]() (如图4).
(如图4).
(1)请用含![]() 的代数式表示
的代数式表示![]() .
.
(2)请用含![]() 的代数式表示
的代数式表示![]() .
.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
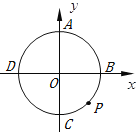
【题目】如图,半径为![]() 且坐标原点为圆心的圆交
且坐标原点为圆心的圆交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 、
、![]() 、
、![]() ,过圆上的一动点
,过圆上的一动点![]() (不与
(不与![]() 重合)作
重合)作![]() ,且
,且![]() (
(![]() 在
在![]()
![]() 右侧)
右侧)
(1)连结![]() ,当
,当![]() 时,则点
时,则点![]() 的横坐标是______.
的横坐标是______.
(2)连结![]() ,设线段
,设线段![]() 的长为
的长为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com