
科目: 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,它的出现标志中国古代数学形成了完整的体系.其中有一个问题:“今有二马、一牛价过-万,如半马之价:一马、二牛价不满一万,如半牛之价.问牛、马价各几何?”其大意为:现有两匹马加一头牛的价钱超过一万,超过的部分正好是半匹马的价钱:一匹马加上两头牛的价钱则不到一万,不足的部分正好是半头牛的价钱.问一头牛、一匹马各多少钱?设一匹马值![]() 钱、一头牛值
钱、一头牛值![]() 钱,则符合题意的方程组为( )
钱,则符合题意的方程组为( )
A. B.
B.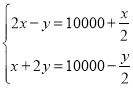
C.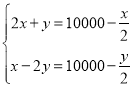 D.
D.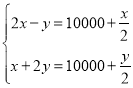
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:
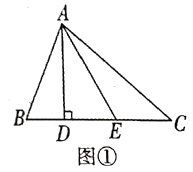
(1)如图①在![]() 中,
中,![]() 是
是![]() 边
边![]() 的高,点
的高,点![]() 是
是![]() 上任意一点,若
上任意一点,若![]() 则
则![]() 的最小值为_ ;
的最小值为_ ;
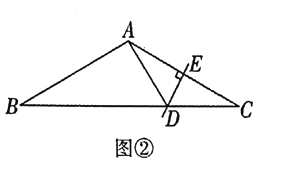
(2)如图②,在等腰![]() 中,
中,![]() 是
是![]() 的垂直平分线,分别交
的垂直平分线,分别交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
问题解决:
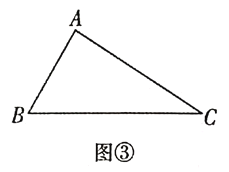
(3)如图③,某公园管理员拟在园内规划一个![]() 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路
区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路![]() 和
和![]() ,满足
,满足![]() 点
点![]() 到
到![]() 的距离为
的距离为![]() .为了节约成本,要使得
.为了节约成本,要使得![]() 之和最短,试求
之和最短,试求![]() 的最小值(路宽忽略不计).
的最小值(路宽忽略不计).
查看答案和解析>>
科目: 来源: 题型:
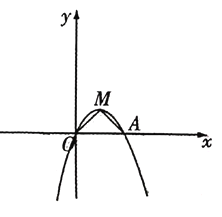
【题目】如图,在平面直角坐标系中,顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() .
.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)已知点![]() 的坐标为
的坐标为![]() ,将抛物线
,将抛物线![]() 向上平移得到抛物线
向上平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() (点
(点![]() 在点
在点![]() 的左侧),如果
的左侧),如果![]() 与
与![]() 相似,求所有符合条件的抛物线
相似,求所有符合条件的抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进人积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
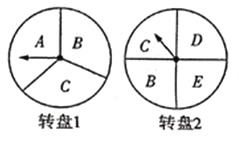
(1)用树状图或列表的方法表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位![]() ),右边为华氏温度的刻度和读数(单位
),右边为华氏温度的刻度和读数(单位![]() ).从温度计的刻度上可以看出,摄氏温度
).从温度计的刻度上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 部分对应关系如下表:
部分对应关系如下表:
| ··· |
|
| ··· |
| ··· |
|
| ··· |

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当摄氏温度为零下![]() 时,求华氏温度为多少?
时,求华氏温度为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年3月24日,工信部发布《关于推动![]() 加快发展的通知》,全力推进
加快发展的通知》,全力推进![]() 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向
网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向![]() 迁移,推动“
迁移,推动“![]() 医疗健康”创新发展,实施“
医疗健康”创新发展,实施“![]() 工业互联网”512工程,促进“
工业互联网”512工程,促进“![]() 车联网”协同发展,构建
车联网”协同发展,构建![]() 应用生态系统.现“
应用生态系统.现“![]() 网络”已成为一个热门词汇,某校为了解九年级学生对“
网络”已成为一个热门词汇,某校为了解九年级学生对“![]() 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
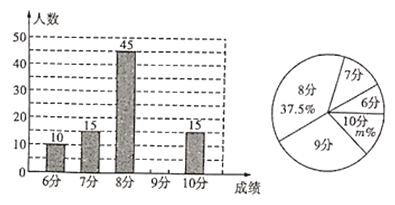
(1)请补全条形统计图,扇形统计图中![]() __;
__;
(2)所调查学生成绩的众数是_ ____分,平均数是_ 分;
(3)若该校九年级学生有![]() 人,请估计得分不少于
人,请估计得分不少于![]() 分的有多少人?
分的有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.
(概念感知)
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 是否是“准黄金”三角形,请说明理由.
是否是“准黄金”三角形,请说明理由.

(问题探究)
(2)如图2,![]() 是“准黄金”三角形,BC是“金底”,把
是“准黄金”三角形,BC是“金底”,把![]() 沿BC翻折得到
沿BC翻折得到![]() ,连AB接AD交BC的延长线于点E,若点C恰好是
,连AB接AD交BC的延长线于点E,若点C恰好是![]() 的重心,求
的重心,求![]() 的值.
的值.
(拓展提升)
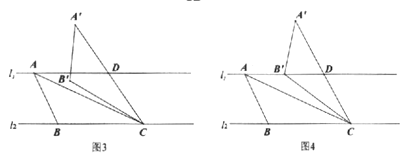
(3)如图3,![]() ,且直线
,且直线![]() 与
与![]() 之间的距离为3,“准黄金”
之间的距离为3,“准黄金”![]() 的“金底”BC在直线
的“金底”BC在直线![]() 上,点A在直线
上,点A在直线![]() 上.
上.![]() ,若
,若![]() 是钝角,将
是钝角,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,线段
,线段![]() 交
交![]() 于点D.
于点D.
①当![]() 时,则
时,则![]() _________;
_________;
②如图4,当点B落在直线![]() 上时,求
上时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于某个函数,若自变量取实数![]() ,其函数值恰好也等于
,其函数值恰好也等于![]() 时,则称
时,则称![]() 为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差
为这个函数的“等量值”.在函数存在“等量值”时,该函数的最大“等量值”与最小“等量值”的差![]() 称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”
称为这个函数的“等量距离”,特别地,当函数只有一个“等量值”时,规定其“等最距离”![]() 为0.
为0.
(1)请分别判断函数![]() ,
,![]() ,
,![]() 有没有“等量值”?如果有,直接写出其“等量距离”;
有没有“等量值”?如果有,直接写出其“等量距离”;
(2)已知函数![]() .
.
①若其“等量距离”为0,求![]() 的值;
的值;
②若![]() ,求其“等量距离”
,求其“等量距离”![]() 的取值范围;
的取值范围;
③若“等量距离”![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
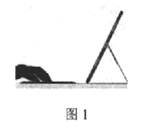
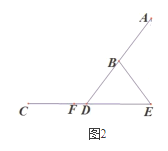
【题目】图1是一台用保护套套好的带键盘的平板电脑实物图,图2是它的示意图,忽略平板电脑的厚度,支架BE分别固定在平板电脑AD背面中点B处,桌面E处,EB可以绕点E转动,当点D在线段EF上滑动时,可调节平板电脑AD的倾斜角![]() ,经测量,
,经测量,![]() ,
,![]() ,支架
,支架![]() .
.
(1)连接AE,求证:![]() ;
;
(2)当![]() 时,求A,E两点间的距离;
时,求A,E两点间的距离;
(3)当点D滑到距离F点1cm处时,视觉效果最好,求此时倾斜角![]() 的度数.
的度数.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,结果保留一位小数)
,结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com