
科目: 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校举办学生综合素质大赛,分“单人项目”和“双人项目”两种形式,比赛题目包括下列五类:![]() .人文艺术;
.人文艺术;![]() .历史社会;
.历史社会;![]() .自然科学;
.自然科学;![]() .天文地理;
.天文地理;![]() .体育健康.
.体育健康.
(1)若小明参加“单人项目”,他从中抽取一个题目,那么恰好抽中“自然科学”类题目的概率为_____.
(2)小林和小丽参加“双人项目”,比赛规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,求他们抽到“天文地理”和“体育健康”类题目的概率是多少?(用画树状图或列表的方法求解).
查看答案和解析>>
科目: 来源: 题型:
【题目】2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
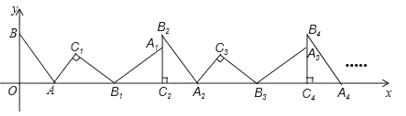
【题目】如图,在平面直角坐标系中,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() ,
,![]() 分别落在点
分别落在点![]() ,
,![]() 处,点
处,点![]() 在
在![]() 轴上,再将
轴上,再将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,将
轴上,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 轴上,依次进行下去……,若点
轴上,依次进行下去……,若点![]() ,
,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,顶点
轴上,顶点![]() 在第二象限,点
在第二象限,点![]() 的坐标为
的坐标为![]() .将线段
.将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至线段
至线段![]() ,若反比例函数y=
,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为_________.
(k≠0)的图象经过A、D两点,则k值为_________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为( ).
边的长为( ).
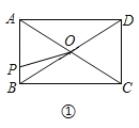
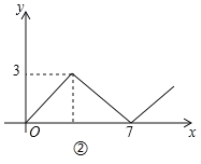
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目: 来源: 题型:
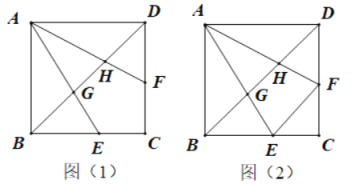
【题目】如图(1),已知正方形ABCD中,点E、F分别在边BC、CD上,BE=DF,AE、AF分别交BD于点G、H.
(1)求证:BG=DH;
(2)连接FE,如图(2),当EF=BG时.
①求证:ADAH=AFDF;
②直接写出![]() 的比值.
的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
销售价格x(元/千克) | 10 | 12 | … | 30 |
市场需求量q(千克) | 30 | 28 | … | 10 |
(已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克)
(1)请写出q与x的函数关系式:___________________________;
(2)当每天的进货量小于或等于市场需求量时,这种海鲜食材能全部售出,而当每天的进货量大于市场需求量时,只能售出符合市场需求量的海鲜食材,剩余的海鲜食材由于保质期短而只能废弃.
①求出每天获得的利润y(元)与销售价格x的函数关系式;
②为了避免浪费,每天要确保这种海鲜食材能全部售出,求销售价格为多少元时,每天获得的利润(元)最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com