
科目: 来源: 题型:
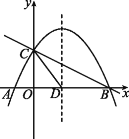
【题目】如图,直线y=-![]() x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
(1)求B,C两点的坐标.
(2)求该二次函数的解析式.
(3)若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.
(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:________.
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数.
查看答案和解析>>
科目: 来源: 题型:
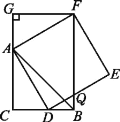
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与点B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC.其中所有正确结论的序号是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知下列命题:①若![]() =-a,则a≤0;②若a>
=-a,则a≤0;②若a>![]() ,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
,则a2>b2;③两个位似图形一定是相似图形;④平行四边形的两组对边分别相等.其中原命题与逆命题均为真命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 分别是边
分别是边![]() 上的动点,连接
上的动点,连接![]() .设
.设![]() (
(![]() ),
),![]() ,
,![]() 与
与![]() 之间的函数关系如图②所示.
之间的函数关系如图②所示.
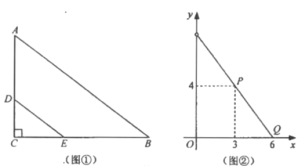
(1)求出图②中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)将![]() 沿
沿![]() 翻折,得
翻折,得![]() .
.
①点![]() 是否可以落在
是否可以落在![]() 的某条角平分线上?如果可以,求出相应
的某条角平分线上?如果可以,求出相应![]() 的值;如果不可以,说明理由;
的值;如果不可以,说明理由;
②直接写出![]() 与
与![]() 重叠部分面积的最大值及相应
重叠部分面积的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
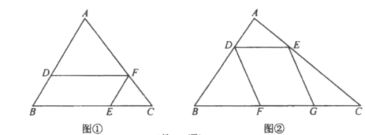
【题目】如图①,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,且
上,且![]() .设
.设![]() 的边
的边![]() 上的高为
上的高为![]() ,
,![]() 的边
的边![]() 上的高为
上的高为![]() .
.
(1)若![]() 、
、![]() 的面积分别为3,1,则
的面积分别为3,1,则![]() ;
;
(2)设![]() 、
、![]() 、四边形
、四边形![]() 的面积分别为
的面积分别为![]() ,求证:
,求证:![]() ;
;
(3)如图②,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() ,
, ![]() . 若
. 若 、
、![]() 、
、![]() 的面积分别为3, 7, 5,求
的面积分别为3, 7, 5,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,己知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,其对称轴与抛物线相交于点
,其对称轴与抛物线相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
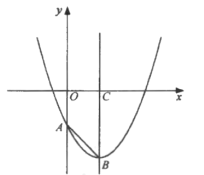
(1)求![]() 的长;
的长;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为![]() .若新抛物线经过原点
.若新抛物线经过原点![]() ,且
,且![]() ,求新抛物线对应的函数表达式.
,求新抛物线对应的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了防控新型冠状病毒,购买了甲、乙两种消毒液进行校园环境消毒.己知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶,共花费3 600元;第二次购买了甲种消毒液60瓶和乙种消毒液40瓶,共花费3 400元.
(1)每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元?
(2)学校准备第三次购买这两种消毒液,其中甲种消毒液比乙种消毒液多10瓶,并且总花费不超过3 500元,最多能购买多少瓶甲种消毒液?
查看答案和解析>>
科目: 来源: 题型:
【题目】学校随机抽取部分学生就“你是否喜欢网课”进行问卷调查,并将调查结果进行统计后,绘制成如下统计表和扇形统计图.
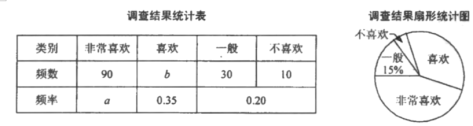
(1)在统计表中,![]() ,
,![]() ;
;
(2)求出扇形统计图中“喜欢”网课所对应扇形的圆心角度数;
(3)己知该校共有2 000名学生,试估计该校“非常喜欢”网课的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com