
科目: 来源: 题型:
【题目】现有![]() 个质地、大小完全相同的小球上分别标有数字
个质地、大小完全相同的小球上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .先将标有数字
.先将标有数字![]() ,
,![]() ,
,![]() 的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现从第一个盒子里随机取出一个小球,再从第二个盒子里随机取出一个小球.两次分别用x、y来表示.
的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现从第一个盒子里随机取出一个小球,再从第二个盒子里随机取出一个小球.两次分别用x、y来表示.
(1)请利用列表或画树状图的方法中的一种方法,求(x,y)所有可能出现的结果总数;
(2)求取出的两个小球上的数字之和等于![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接2020年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给信息,解答下列问题:
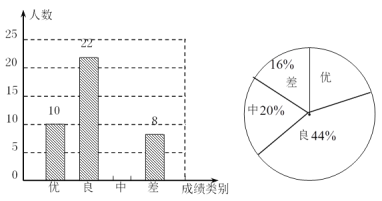
(1)请将表示成绩类别为“中”的条形统计图补充完整;
(2)请将表示成绩类别为“优”的扇形统计图补充完整,并计算成绩类别为“优”的扇形所对应的圆心角的度数;
(3)学校九年级共有![]() 人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀.
人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 是等腰直角三角形且
是等腰直角三角形且![]() ,把
,把![]() 绕点B顺时针旋转
绕点B顺时针旋转![]() ,得到
,得到![]() ,把
,把![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() ,得到
,得到![]() ,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
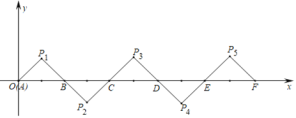
A.(4039,-1)
B.(4039,1)
C.(2020,-1)
D.(2020,1)
查看答案和解析>>
科目: 来源: 题型:
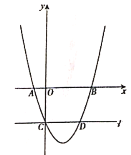
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,经过点
,经过点![]() 的直线
的直线![]() 与该抛物线交于另一点
与该抛物线交于另一点![]() ,并且直线
,并且直线![]() 轴,点
轴,点![]() 为该抛物线上一个动点,点
为该抛物线上一个动点,点![]() 为直线
为直线![]() 上一个动点.
上一个动点.
(1)当![]() ,且
,且![]() 时,连接
时,连接![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是平行四边形
是平行四边形
(2)当![]() 时,连接
时,连接![]() ,线段
,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)连接![]() ,
,![]() ,试探究:是否存在点
,试探究:是否存在点![]() ,使得
,使得![]() 与
与![]() 互为余角?若存在,求出点
互为余角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(3)延长线段![]() 到
到![]() ,延长线段
,延长线段![]() 到
到![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①判断![]() 的形状,并说明理由;
的形状,并说明理由;
②若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
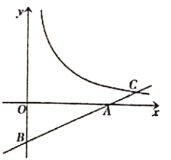
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于
轴分别相交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 的横坐标为4.
的横坐标为4.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 是该反比例函数
是该反比例函数![]() 的图象上一点,连接
的图象上一点,连接![]() ,
,![]() ,且
,且![]() .
.
①求点![]() 的坐标;
的坐标;
②求点![]() 到直线
到直线![]() 的距离
的距离![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,要求被调查的市民必选且只能选一项.根据调查结果绘制了如图尚不完整的扇形统计图,其中将“手机上网”和“电脑上网”作为“获取新闻的最主要途径”的市民分别有600人和510人,并且扇形统计图中![]() ,
,![]() 满足
满足![]() .请根据所给信息,解答下列问题:
.请根据所给信息,解答下列问题:

(1)请计算扇形统计图中“电脑上网”所在扇形的圆心角的度数;
(2)求扇形统计图中![]() ,
,![]() 的值;
的值;
(3)若该市约有200万人,请你估计其中将“手机上网”和“报纸”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),以下结论: ①
之间(包含端点),以下结论: ①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 没有实数根.其中正确的结论有( )
没有实数根.其中正确的结论有( )
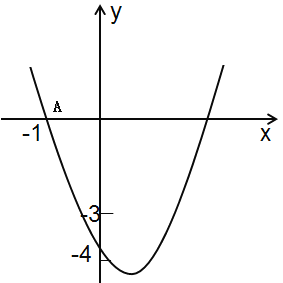
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com