
科目: 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).

(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题12分)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.

(1)求证:CD为⊙O的切线;
(2)求证:∠C=2∠DBE.
(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于C、D两点,与x轴交于点A.
交于C、D两点,与x轴交于点A.
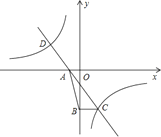
(1)求n的取值范围和点A的坐标;
(2)过点C作CB⊥y轴,垂足为B,若S△ABC=4,求双曲线的解析式;
(3)在(1)、(2)的条件下,若AB=![]() ,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
,求点C和点D的坐标并根据图象直接写出反比例函数的值小于一次函数的值时,自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
科目: 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 .
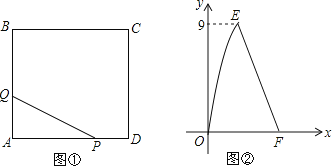
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的个数是( )
①为了了解一批灯泡的使用寿命,应采用全面调查的方式
②一组数据5,6,7,6, 8,10的众数和中位数都是6
③已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是m≥0
④式子![]() 有意义的条件是
有意义的条件是![]()
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
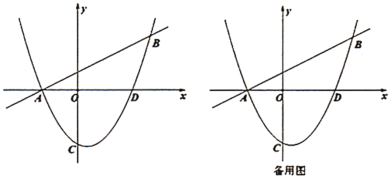
【题目】如图,一次函数![]() 的图像与二次函数
的图像与二次函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 的横坐标为4.
的横坐标为4.
(1)![]() ________,
________,![]() ________;
________;
(2)设二次函数的图像与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)①若![]() 点在
点在![]() 轴下方二次函数图像上,过
轴下方二次函数图像上,过![]() 点作
点作![]() 轴平行线交直线
轴平行线交直线![]() 于点
于点![]() ,以
,以![]() 点为圆心,
点为圆心,![]() 的长为半径画圆,求
的长为半径画圆,求![]() 在直线
在直线![]() 上截得的弦长的最大值.
上截得的弦长的最大值.
②若∠ABM=∠ACO,则点M的坐标为_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com