
科目: 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点在
的顶点在![]() 上,
上,![]() 交直线
交直线![]() 于
于![]() 点.
点.
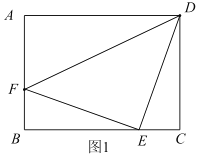

(1)如图1,若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
(2)如图2,![]() ,当
,当![]() 时,求证:
时,求证:![]() 是
是![]() 的中点;
的中点;
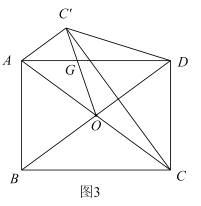
(3)如图3,若![]() ,对角线
,对角线![]() ,
,![]() 交于点
交于点![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,求
,求![]() 的长,请直接写出答案.
的长,请直接写出答案.
查看答案和解析>>
科目: 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() 即
即![]()
∴![]() ∴
∴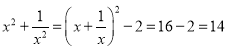
材料二:在解决某些连等式问题时,通常可以引入参数“![]() ”,将连等式变成几个值为
”,将连等式变成几个值为![]() 的等式,这样就可以通过适当变形解决问题.
的等式,这样就可以通过适当变形解决问题.
例:若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:令![]() 则
则![]() ,
,![]() ,
,![]() ,∴
,∴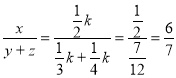
根据材料回答问题:
(1)已知![]() ,求
,求![]() 的值.
的值.
(2)已知![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线OE的对称点,是否存在点
关于直线OE的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 上?若存在,请直接写出相应的点
上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】乐高积木是儿童喜爱的玩具.这种塑胶积木一头有凸粒,另一头有可嵌入凸粒的孔,形状有1300多种,每一种形状都有12种不同的颜色,以红、黄、蓝、白、绿色为主.它靠小朋友自己动手动脑,可以拼插出变化无穷的造型,令人爱不释手,被称为“魔术塑料积木”.某玩具店购进一批甲、乙两款乐高积木,它们的进货单价之和是720元.甲款积木零售单价比进货单价多80元.乙款积木零售价比进货单价的1.5倍少120元,按零售单价购买甲款积木4盒和乙款积木2盒,共需要2640元.
(1)分别求出甲乙两款积木的进价;
(2)该玩具店平均一个星期卖出甲款积木40盒和乙款积木24盒,经调查发现,甲款积木零售单价每降低2元,平均一个星期可多售出甲款积木4盒,商店决定把甲款积木的零售价下降![]() 元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当
元,乙款积木的零售价和销量都不变.在不考虑其他因素的条件下,为了顾客能获取更多的优惠,当![]() 为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
为多少时,玩具店一个星期销售甲、乙两款积木获取的总利润为5760元.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
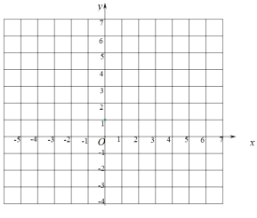
(1)根据给定的条件,则![]() _________,
_________,![]() ____________.
____________.
(2)在给出的平面直角坐标系中,画出函数图像;
(3)①结合所画的图像,直接写出方程![]() 的解,解为________________.(精确到十分位)
的解,解为________________.(精确到十分位)
②若一次函数![]() 的图像与
的图像与![]() 的图像有且只有三个交点,则
的图像有且只有三个交点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】面对疫情,每个人都需要积极行动起来,做好预防工作.为此某校开展了“新型冠状病毒肺炎”防控知识竞赛.现从该校五、六年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用![]() 表示,共分成四组:A.
表示,共分成四组:A.![]() ,B.
,B.![]() ,C.
,C.![]() ,D.
,D.![]() ),下面给出了部分信息:
),下面给出了部分信息:
五年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
六年级10名学生的竞赛成绩在C组中的数据是:94,90,94
五、六年级抽取的学生竞赛成绩统计表
年级 | 平均数 | 中位数 | 众数 | 方差 |
五年级 | 92 | 93 |
| 52 |
六年级 | 92 |
| 100 | 50.4 |
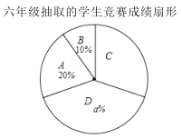
是据以上信息,解答下列问题:
(1)直接写出上述图表中![]() ,
,![]() ,
,![]() 的值:
的值:![]() __________,
__________,![]() ___________,
___________,![]() ___________;
___________;
(2)由以上数据,你认为该校五、六年级中哪个年级学生掌握防溺水安全知识较好?请说明理由(一条理由即可);
(3)该校五、六年级共1800人参加了此次竞赛活动,估计参加此次竞赛活动成绩优秀![]() 的学生人数是多少?
的学生人数是多少?
查看答案和解析>>
科目: 来源: 题型:
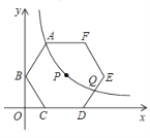
【题目】如图,在平面直角坐标系中,正六边形![]() 的对称中心
的对称中心![]() 在反比例函数
在反比例函数![]() 的图象上,边
的图象上,边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,已知
轴上,已知![]() .若该反比例函数图象与
.若该反比例函数图象与![]() 交于点
交于点![]() ,则点的
,则点的![]() 横坐标是_________.
横坐标是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目: 来源: 题型:
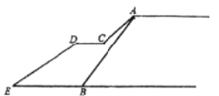
【题目】如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图.起初工程师计划修建一段坡度为3:2的扶梯![]() ,扶梯总长为
,扶梯总长为![]() 米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建
米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建![]() 、
、![]() 两段扶梯,并减缓各扶梯的坡度,其中扶梯
两段扶梯,并减缓各扶梯的坡度,其中扶梯![]() 和平台
和平台![]() 形成的
形成的![]() 为135°,从
为135°,从![]() 点看
点看![]() 点的仰角为36.5°,
点的仰角为36.5°,![]() 段扶梯长
段扶梯长![]() 米,则
米,则![]() 段扶梯长度约为( )米(参考数据:
段扶梯长度约为( )米(参考数据:![]() ,
,![]() ,
,![]() )
)
A.43B.45C.47D.49
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() .
.
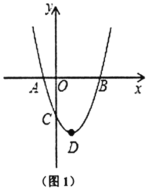
(1)抛物线顶点![]() 的坐标为________;
的坐标为________;
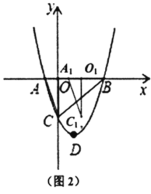
(2)如图2,连接![]() 、
、![]() .将
.将![]() 沿
沿![]() 轴方向以每秒1个单位长度的速度向右平移得到
轴方向以每秒1个单位长度的速度向右平移得到![]() ,运动时间为
,运动时间为![]() 秒.当
秒.当![]() 时,求
时,求![]() 与
与![]() 重叠面积
重叠面积![]() 与
与![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值;
的最大值;
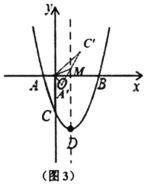
(3)如图3中,将![]() 绕点
绕点![]() 顺时针旋转一定的角度
顺时针旋转一定的角度![]() 得到
得到![]() ,边
,边![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() .在旋转过程中,是否存在一点
.在旋转过程中,是否存在一点![]() ,使得
,使得![]() ?若存在,直接写出所有满足条件的点
?若存在,直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com