
科目: 来源: 题型:
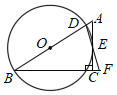
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.
(1)求证:BD=BF;
(2)填空:
①若⊙O的半径为5,tanB=![]() ,则CF= ;
,则CF= ;
②若⊙O与BF相交于点H,当∠B的度数为 时,四边形OBHE为菱形.
查看答案和解析>>
科目: 来源: 题型:
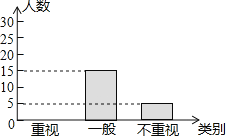
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
查看答案和解析>>
科目: 来源: 题型:
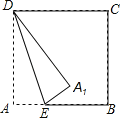
【题目】如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为A(1,0),等腰直角三角形ABC的边AB在x轴的正半轴上,∠ABC=90°,点B在点A的右侧,点C在第一象限.将△ABC绕点A逆时针旋转75°,如果点C的对应点E恰好落在y轴的正半轴上,那么点C的坐标为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,对于点![]() 和
和![]() ,给出如下定义:
,给出如下定义:
如果 ,那么称点
,那么称点![]() 为点
为点![]() 的“伴随点”.
的“伴随点”.
例如:点![]() 的“伴随点”为点
的“伴随点”为点![]() ;点
;点![]() 的“伴随点”为点
的“伴随点”为点![]() .
.
(1)直接写出点![]() 的“伴随点”
的“伴随点”![]() 的坐标.
的坐标.
(2)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标为2,求函数
的纵坐标为2,求函数![]() 的解析式.
的解析式.
(3)点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的“伴随点”为
的“伴随点”为![]() .若点
.若点![]() 在第一象限,且
在第一象限,且![]() ,求此时“伴随点”
,求此时“伴随点”![]() 的横坐标.
的横坐标.
(4)点![]() 在函数
在函数![]() 的图象上,若其“伴随点”
的图象上,若其“伴随点”![]() 的纵坐标
的纵坐标![]() 的最大值为
的最大值为![]() ,直接写出实数
,直接写出实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
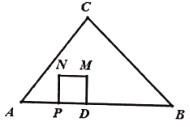
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D在边AB上,且
,点D在边AB上,且![]() ,动点P从点A出发,以每秒1个单位长度的速度向终点B运动,以PD为边向上做正方形
,动点P从点A出发,以每秒1个单位长度的速度向终点B运动,以PD为边向上做正方形![]() ,设点P运动的时间为
,设点P运动的时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
(1)用含有![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(4)当点P在线段AD上运动时,做点N关于CD的对称点![]() ,当
,当![]() 与
与![]() 的某一个顶点的连线平分
的某一个顶点的连线平分![]() 的面积时,求
的面积时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
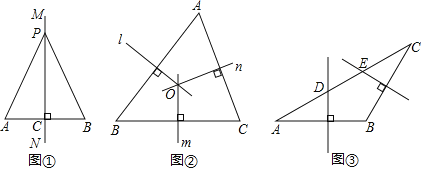
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目: 来源: 题型:
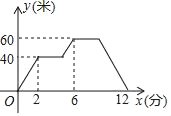
【题目】小明在练习操控航拍无人机,该型号无人机在上升和下落时的速度相同,设无人机的飞行高度为y(米),小明操控无人飞机的时间为x(分),y与x之间的函数图象如图所示.
(1)无人机上升的速度为 米/分,无人机在40米的高度上飞行了 分.
(2)求无人机下落过程中,y与x之间的函数关系式.
(3)求无人机距地面的高度为50米时x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
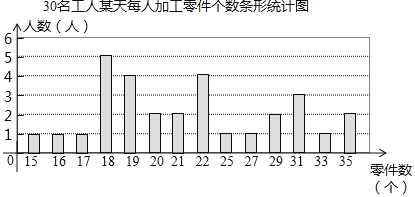
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com