
科目: 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 交x轴于A、B两点,其中点A坐标为
交x轴于A、B两点,其中点A坐标为![]() ,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
(1)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(2)当![]() 时,求b的值;
时,求b的值;
(3)在(1)的条件下,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线![]() 、
、![]() 分别交抛物线的对称轴于点M、N.请问
分别交抛物线的对称轴于点M、N.请问![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
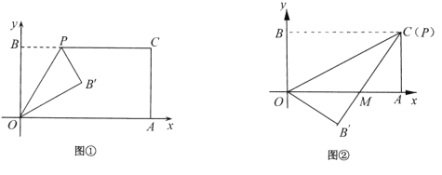
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解本校初中学生在学校号召的“积极公益”活动中周末参加公益的时间(单位:h),随机调查了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
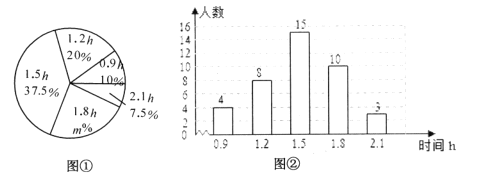
(1)本次接受调查的初中学生人数为________,图①中m的值为________;
(2)求统计的这部分学生参加公益的时间数据的平均数、众数和中位数;
(3)根据统计的这部分学生周末参加公益时间的样本数据,若该校共有650名初中学生,估计该校在这个周末参加公益时间大于1h的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组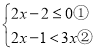
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
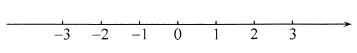
(4)原不等式组的解集为_______________.
查看答案和解析>>
科目: 来源: 题型:
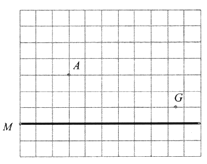
【题目】如图,在每个小正方形的边长为1的网格中,A,M,N均在格点上.在线段![]() 上有一动点B,以
上有一动点B,以![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一个小正方形边的中点.
,G是一个小正方形边的中点.
(1)当点B的位置满足![]() 时,求此时
时,求此时![]() 的长_______;
的长_______;
(2)请用无刻度的直尺,在如图所示的网格中,画出一个点C,使其满足线段![]() 最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系内,抛物线![]() 与线段
与线段![]() 有两个不同的交点,其中点
有两个不同的交点,其中点![]() ,点
,点![]() .有下列结论:
.有下列结论:
①直线![]() 的解析式为
的解析式为![]() ;②方程
;②方程![]() 有两个不相等的实数根;③a的取值范围是
有两个不相等的实数根;③a的取值范围是![]() 或
或![]() .
.
其中,正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
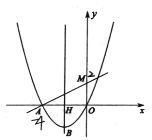
【题目】如图,已知二次函数![]() 的图像经过点
的图像经过点![]() ,顶点为
,顶点为![]() 一次函数
一次函数 ![]() 的图像交
的图像交![]() 轴于点
轴于点![]() 是抛物线上-一点,点
是抛物线上-一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好落在抛物线的对称轴直线
恰好落在抛物线的对称轴直线![]() 上(对称轴直线
上(对称轴直线![]() 与
与![]() 轴交于点
轴交于点![]() ).
).
(1)求二次函数的表达式;
(2)求点![]() 的坐标;
的坐标;
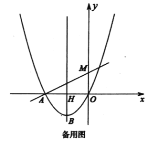
(3)若点![]() 是第二象限内抛物线上一点,
是第二象限内抛物线上一点,![]() 关于抛物线的对称轴的对称点是
关于抛物线的对称轴的对称点是![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是坐标平面内一点,若四边形
是坐标平面内一点,若四边形![]() 是正方形,求点
是正方形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com