
科目: 来源: 题型:
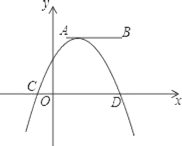
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )
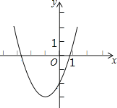
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
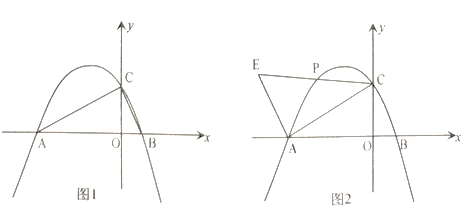
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】[阅读理解]
当![]() 且
且![]() 时,因为
时,因为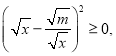 所以
所以![]() 从而
从而![]() (当且仅当
(当且仅当![]() 时取等号).由此可知,在
时取等号).由此可知,在![]() 且
且![]() 的条件下,当
的条件下,当![]() 时,代数式
时,代数式![]() 有最小值为
有最小值为![]() .
.
[实践应用]
(1)在![]() 的条件下,当
的条件下,当![]() 时,
时,![]() 有最小值,且最小值为 ;
有最小值,且最小值为 ;
(2)设![]() ,求
,求![]() 的最小值,并指出当
的最小值,并指出当![]() 取得该最小值时对应的
取得该最小值时对应的![]() 的值;
的值;
[拓展延伸]
在平面直角坐标系中,点![]() 点
点![]() .点
.点![]() 是函数
是函数![]() 在第一象限内图象上的一个动点,过
在第一象限内图象上的一个动点,过![]() 点作
点作![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别为点
轴,垂足分别为点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.

(3)求![]() 和
和![]() 之间的函数关系式:
之间的函数关系式:
(4)试判断当![]() 的值最小时,四边形
的值最小时,四边形![]() 是何特殊四边形,并说明理由.
是何特殊四边形,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某扶贫工作队为一贫困户提供了![]() 万元的无息脱贫贷款.该贫困户利用这笔贷款,注册了一家网店,销售一种成本价为
万元的无息脱贫贷款.该贫困户利用这笔贷款,注册了一家网店,销售一种成本价为![]() 元/件的农产品.已知销售价高于成本价,且不高于
元/件的农产品.已知销售价高于成本价,且不高于![]() 元/件,网店每月需支付电费等其它费用
元/件,网店每月需支付电费等其它费用![]() 千元市场调查发现,该农产品每月销售量为
千元市场调查发现,该农产品每月销售量为![]() (百件)与销售价
(百件)与销售价![]() (元/件)之间的函数关系如图所示
(元/件)之间的函数关系如图所示
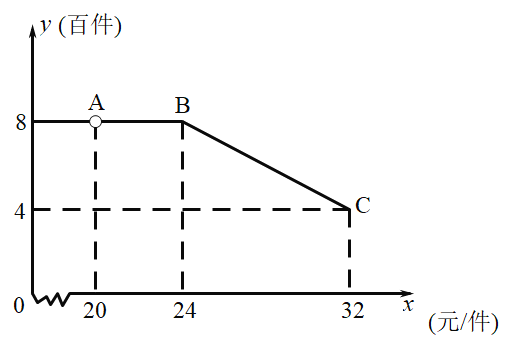
(1)求该网店每月利润![]() (百元)与销售价
(百元)与销售价![]() (元/件)之间的函数关系式,并注明自变量
(元/件)之间的函数关系式,并注明自变量![]() 的取值范围:
的取值范围:
(2)该贫困户从网店开业起,最快在第几个月可用销售利润还清无息贷款?
查看答案和解析>>
科目: 来源: 题型:
【题目】张老师将“校园诗词大赛”所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图,部分信息如下:
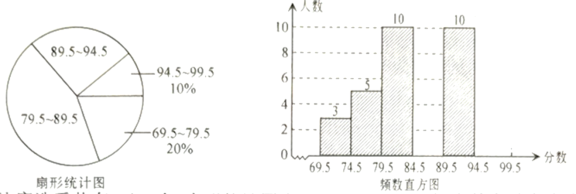
(1)本次比赛选手共有_ 人,扇形统计图中“![]() ”这一组人数占总参赛人数的百分比为_ ,频数直方图中“
”这一组人数占总参赛人数的百分比为_ ,频数直方图中“![]() ”这一组的人数为__ ;
”这一组的人数为__ ;
(2)赛前规定,成绩由高到低前![]() 的参赛选手获奖某参赛选手的比赛成绩为
的参赛选手获奖某参赛选手的比赛成绩为![]() 分,试判断他能否获奖,并说明理由;
分,试判断他能否获奖,并说明理由;
(3)成绩前四名是![]() 名男生和
名男生和![]() 名女生,若从他们中任选
名女生,若从他们中任选![]() 人作为全区“诗词大会”重点培训对象,试求恰好选中
人作为全区“诗词大会”重点培训对象,试求恰好选中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(不与
上(不与![]() 重合),将矩形沿
重合),将矩形沿![]() 折叠,使点
折叠,使点![]() 分别落在点
分别落在点![]() 处有下列结论:
处有下列结论:
①![]() 与
与![]() 互余;
互余;
②若![]() 平分
平分![]() 则
则![]()
③若直线![]() 经过点
经过点![]() 则
则![]()
④若直线![]() 交边
交边![]()
![]() 分别于
分别于![]() 当
当![]() 为等腰三角形时,五边形
为等腰三角形时,五边形![]() 的周长为
的周长为![]() .其中正确结论的序号是_____________________.
.其中正确结论的序号是_____________________.

查看答案和解析>>
科目: 来源: 题型:
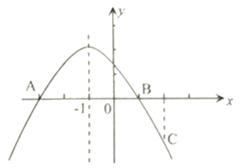
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 点
点![]() ,点
,点![]() 点
点![]() 是抛物线上任意一点,有下列结论:①
是抛物线上任意一点,有下列结论:①![]() ; ②一元二次方程
; ②一元二次方程![]() 的两个根为
的两个根为![]() 和
和![]() ;③若
;③若![]() ,则
,则![]() ;④对于任意实数
;④对于任意实数![]()
![]() 总成立.其中正确结论的个数为 ( )
总成立.其中正确结论的个数为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求![]() 的值;
的值;
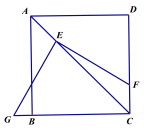
(2)如图,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
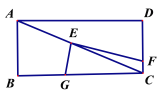
(3)如图,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,直接写出EG、EF 的长.
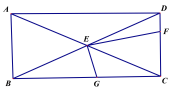
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com