
科目: 来源: 题型:
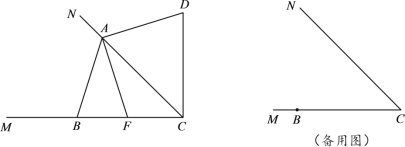
【题目】已知∠MCN=45°,点B在射线CM上,点A是射线CN上的一个动点(不与点C重合).点B关于CN的对称点为点D,连接AB、AD和CD,点F在直线BC上,且满足AF⊥AD.小明在探究图形运动的过程中发现AF=AB:始终成立.
![]() 如图,当0°<∠BAC<90°时.
如图,当0°<∠BAC<90°时.
① 求证:AF=AB;
② 用等式表示线段![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
![]() 当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
当90°<∠BAC<135°时,直接用等式表示线段CF、CD与CA之间的数量关系是 .
查看答案和解析>>
科目: 来源: 题型:
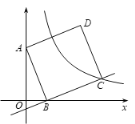
【题目】如图,在直角坐标系中,正方形ABCD绕点A(0,6)旋转,当点B落在x轴上时,点C刚好落在反比例函数![]() (k≠0,x>0)的图像上.已知sin∠OAB=
(k≠0,x>0)的图像上.已知sin∠OAB=![]() .
.
(1)求反比例函数的表达式;
(2)反比例函数![]() 的图像是否经过AD边的中点,并说明理由.
的图像是否经过AD边的中点,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市实施城乡生活垃圾分类管理,推进生态文明建设. 为增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为A,B,C,D,E,F,G,H,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.

⑴ 求8名学生中至少有三类垃圾投放正确的概率;
⑵ 为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果,并求出刚好抽到C、G两位学生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目: 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
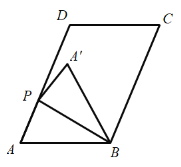
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
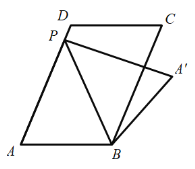
(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
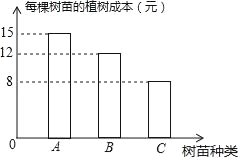
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,过点
上的点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为直径作半圆
为直径作半圆![]() .
.
(1)填空:点![]() _____________(填“在”或“不在”)
_____________(填“在”或“不在”)![]() 上;当
上;当![]() 时,
时,![]() 的值是_____________;
的值是_____________;
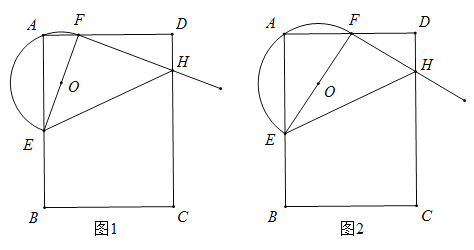
(2)如图1,在![]() 中,当
中,当![]() 时,求证:
时,求证:![]() ;
;
(3)如图2,当![]() 的顶点
的顶点![]() 是边
是边![]() 的中点时,请直接写出
的中点时,请直接写出![]() 三条线段的数量关系.
三条线段的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某社区工作人员在社区随机抽取了若干名居民开展环保知识有奖问答活动,并用得到的数据绘制了如图所示条形统计图(得分为整数,满分为10分,最低分为6分).
请根据图中信息,解答下列问题:
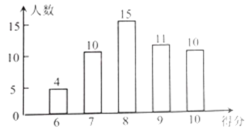
(1)本次调查一共抽取了__________名居民;
(2)求本次调查获取的样本数据的平均数;并直接写出样本数据的众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”.根据调查结果,请你帮社区工作人员直接估计出需准备多少份“一等奖”奖品.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于四个数“![]() ,
,![]() ,
,![]() ,
,![]() ”及四种运算“
”及四种运算“![]() ,
,![]() ,
,![]() ,
,![]() ”,列算式解答:
”,列算式解答:
(1)求这四个数的和;
(2)在这四个数中选出两个数,按要求进行下列计算,使得:
①两数差的结果最小;
②两数积的结果最大;
(3)在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,使运算结果等于没选的那个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com