
科目: 来源: 题型:
【题目】已知抛物线y=﹣x2+2bx+1﹣2b(b为常数).
(1)若点(2,5)在该抛物线上,求b的值;
(2)若该抛物线的顶点坐标是(m,n),求n关于m的函数解析式;
(3)若抛物线与x轴交点之间的距离大于4,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取![]() 名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩频数分布直方图
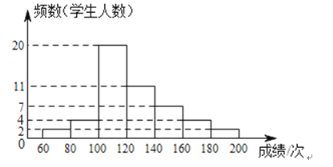
七、八年级学生一分钟跳绳成绩分析表

七年级学生一分钟跳绳成绩(数据分![]() 组:
组:![]() )在
)在![]() 这一组的是:
这一组的是:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
根据以上信息,回答下列问题:
![]() 表中
表中![]() ;
;
![]() 在这次测试中,七年级甲同学的成绩
在这次测试中,七年级甲同学的成绩![]() 次,八年级乙同学的成绩
次,八年级乙同学的成绩![]() ,他们的测试成绩,在各自年级所抽取的
,他们的测试成绩,在各自年级所抽取的![]() 名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
![]() 该校七年级共有
该校七年级共有![]() 名学生,估计一分钟跳绳不低于
名学生,估计一分钟跳绳不低于![]() 次的有多少人?
次的有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个黑球和2个红球,这些球除颜色外都相同.顾客每次摸出一个球,若摸到黑球,则获得1份奖品;若摸到红球,则没有奖品.
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=2,AD=3.E,F分别是AD,CD上的动点,EF=2.Q是EF的中点,P为BC上的动点,连接AP,PQ.则AP+PQ的最小值等于( )
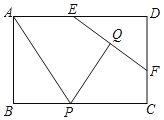
A.2B.3C.4D.5
查看答案和解析>>
科目: 来源: 题型:
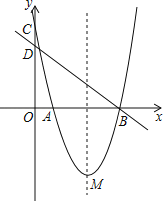
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与两坐标轴分别交于点A、B、C,直线y=﹣![]() x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
x+4经过点B,与y轴交点为D,M(3,﹣4)是抛物线的顶点.
(1)求抛物线的解析式.
(2)已知点N在对称轴上,且AN+DN的值最小.求点N的坐标.
(3)在(2)的条件下,若点E与点C关于对称轴对称,请你画出△EMN并求它的面积.
(4)在(2)的条件下,在坐标平面内是否存在点P,使以A、B、N、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
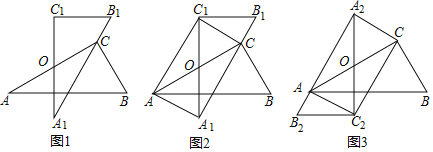
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点O是边AC的中点.
(1)在图1中,将△ABC绕点O逆时针旋转n°得到△A1B1C1,使边A1B1经过点C.求n的值.
(2)将图1向右平移到图2位置,在图2中,连结AA1、AC1、CC1.求证:四边形AA1CC1是矩形;
(3)在图3中,将△ABC绕点O顺时针旋转m°得到△A2B2C2,使边A2B2经过点A,连结AC2、A2C、CC2.
①请你直接写出m的值和四边形AA2CC2的形状;
②若AB=![]() ,请直接写出AA2的长.
,请直接写出AA2的长.
查看答案和解析>>
科目: 来源: 题型:
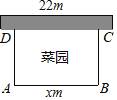
【题目】如图,用一段长为30m的篱笆围成一个一边靠墙的矩形菜园(矩形ABCD),墙长为22m,这个矩形的长AB=xm,菜园的面积为Sm2,且AB>AD.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围.
(2)若要围建的菜园为100m2时,求该莱园的长.
(3)当该菜园的长为多少m时,菜园的面积最大?最大面积是多少m2?
查看答案和解析>>
科目: 来源: 题型:
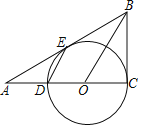
【题目】如图,点D、O在△ABC的边AC上,以CD为直径的⊙O与边AB相切于点E,连结DE、OB,且DE∥OB.
(1)求证:BC是⊙O的切线.
(2)设OB与⊙O交于点F,连结EF,若AD=OD,DE=4,求弦EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com