
科目: 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
(1)求该车间的日废水处理量m;
(2)为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论

查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.

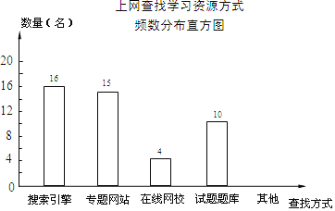
(1)频数分布表中![]() 的值:
的值:![]() _____________,
_____________,![]() ______________;
______________;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() (
(![]() 是常数,
是常数,![]() )与
)与![]() 轴交于
轴交于![]() 两点,顶点
两点,顶点![]() 给出下列结论:①
给出下列结论:①![]() ;②若
;②若![]() 在抛物线上,则
在抛物线上,则![]() ;③关于
;③关于![]() 的方程
的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,
时,![]() 为等腰直角三角形,其中正确的结论是( )
为等腰直角三角形,其中正确的结论是( )
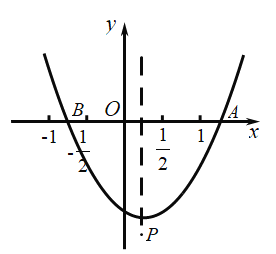
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,汽车以速度V(m/s)匀速行驶,若一路绿灯通过路口A、B、C、D且10≤V≤25,则称V为绿灯速度.已知各路口红灯、绿灯均每隔30 s交替一次,其余因素忽略不计.

(图1)
I.从红绿灯设置到绿灯速度
设汽车在第0秒出发,行驶t s后路程为S m.图2表示在某种红绿灯设置下汽车行驶的情况.
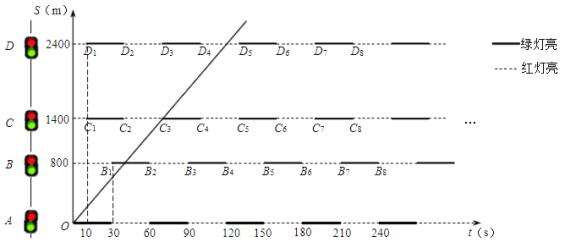
(图2)
(1)路段BC的长度为______m,路口A绿灯亮起______s后路口D绿灯亮起;
(2)求出射线OC3所对应的V的值,判断此时V是否为绿灯速度,并说明理由;
(3)写出这种红绿灯设置下绿灯速度的取值范围,并在图2中画出对应的示意图
II.从绿灯速度到红绿灯设置
(4)当V=20时,汽车经过的每个路口绿灯都恰好开始亮起.根据题意,在图3中画图表示各路口的红绿灯设置.
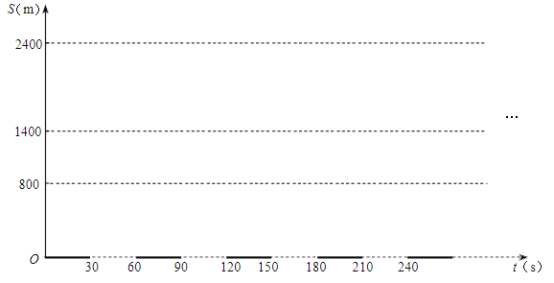 (图3)
(图3)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接DE,P是DE上一点,∠BPC=90°,延长CP交AD于点F.⊙O经过P、D、F,交CD于点G.
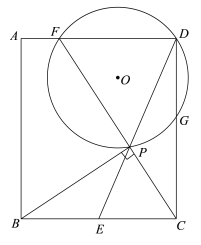
(1)求证:DF![]() DP;
DP;
(2)若![]() ,
,![]() ,求DG的长;
,求DG的长;
(3)连接BF,若BF是⊙O的切线,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2-6ax+5a(a为常数)的图像为抛物线C.
(1)求证:不论a为何值,抛物线C与x轴总有两个不同的公共点;
(2)设抛物线C交x轴于点A、B,交y轴于点D,若△ABD的面积为20,求a的值;
(3)设点E(2,4)、F(3,4),若抛物线C与线段EF只有一个公共点,结合函数图像,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com