
科目: 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目: 来源: 题型:
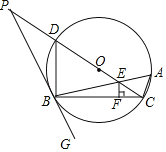
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
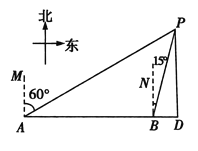
【题目】一艘轮船向正东方向航行,在A处测得灯塔P在A的北偏东60°方向,航行40海里到达B处,此时测得灯塔P在B的北偏东15°方向.
(1)求灯塔P到轮船航线的距离PD;(结果保留根号)
(2)当轮船从B处继续向东航行时,一艘快艇从灯塔P处同时前往D处,尽管快艇速度是轮船速度的2倍,但快艇还是比轮船晚15分钟到达D处,求轮船每小时航行多少海里.(结果精确到1海里,参考数据![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目: 来源: 题型:
【题目】“校园安全”越来越受到人们的关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:

(1)接受问卷调查的学生共有______人,条形统计图中m的值为______;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为______;
(3)若该中学共有学生1800人,根据上述调查结果,可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为______人;
(4)若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E。那么点D的坐标为( )
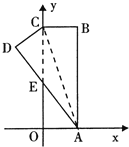
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x=![]() 与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<
与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<![]() 时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是
时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是

A. ②③④ B. ①②③ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB = ∠EDF = 90°,∠DEF = 45°,AC = 8 cm,BC = 6 cm,EF = 9 cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
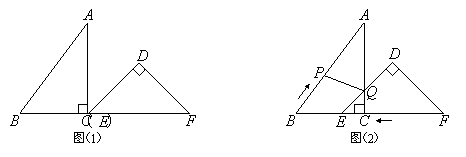
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com