
科目: 来源: 题型:
【题目】阅读下面内容,并解决问题:
《名画》中的数学
前苏联著名科学家别莱利曼在他所著的《趣味代数学》中介绍了波格达诺夫·别列斯基的《名画》,画上那位老师拉金斯基是一位自然科学教授,放弃了大学教席(教师职务)来到农村学校当一名普通老师.画中,黑板上写着一道式子,如图所示:

从这道算式计算可以得出答案等于2,如果仔细一研究,10,11,12,13,14这几个数具有一种有趣的特性:![]() ,而且
,而且![]() .
.
请解答以下问题:
(1)还有没有其他像这样五个连续的整数,前三个数的平方和正好等于后两个数的平方和呢?如果有,请求出另外的五个连续的整数;
(2)若七个连续整数前四个数的平方和等于后三个数的平方和,请直接写出符合条件的连续整数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(4,5),C(3,2).(正方形网格中,每个小正方形的边长都是1个单位长度)
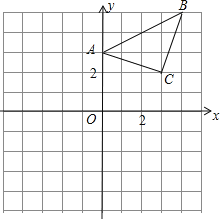
(1)画出△ABC向下平移5个单位长度得到的![]() ,并直接写出点
,并直接写出点![]() 的坐标;
的坐标;
(2)以点B为位似中心,在网格中画出![]() ,使
,使![]() 与
与![]() 位似,且相似比为2∶1,并直接写出
位似,且相似比为2∶1,并直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]()
![]() 轴于点
轴于点![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,运动时间
轴的正方向运动,运动时间![]()
![]() .过点
.过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
(1)当![]() 时,试求
时,试求![]() 的值;
的值;
(2)当![]() 为
为![]() 中点时,试求
中点时,试求![]() 的值;
的值;
(3)是否存在这样的![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,求出所有符合条件的
的面积相等?若存在,求出所有符合条件的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
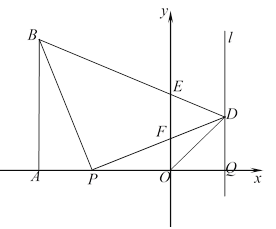
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,且其三个顶点均在抛物线
,且其三个顶点均在抛物线![]() 上.
上.
(1)求抛物线的解析式;
(2)若过原点![]() 的直线
的直线![]() 与直线
与直线![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() ,
,
①当![]() 时,试求
时,试求![]() 的面积;
的面积;
②试证明:不论实数![]() 取何值,直线
取何值,直线![]() 总是经过一定点.
总是经过一定点.
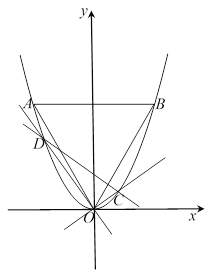
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 延长线上的动点,过点
延长线上的动点,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点,
为切点, ![]() 为
为![]() 上的动点,连接
上的动点,连接![]() 交
交![]() 于点
于点![]() .
.
(1)当![]() 平分
平分![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() ;
;
(3)当![]() ,且
,且![]() 的周长被
的周长被![]() 平分时,设
平分时,设![]() ,试求
,试求![]() 的值.
的值.
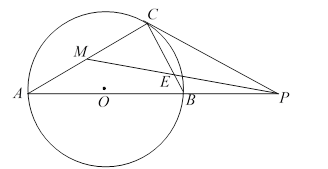
查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读材料,再解答问题:
已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.例如:求点
计算.例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线![]() 可知:
可知:![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]() .
.
求:(1)已知直线![]() 与
与![]() 平行,求这两条平行线之间的距离;
平行,求这两条平行线之间的距离;
(2)已知直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 为
为![]() 上的动点,试求
上的动点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】袋中有四张卡片,其中两张红色卡片![]() ,标号分别为
,标号分别为![]() ;两张蓝色卡片
;两张蓝色卡片![]() ,标号分别为
,标号分别为![]() .
.
(1)从以上四张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率;
的概率;
(2)向袋中再放入一张绿色卡片![]() ,标号记为
,标号记为![]() ,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于
,从这五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.“明天降雨的概率是![]() ”表示明天有半天都在降雨
”表示明天有半天都在降雨
B.数据10,9,8,7,9,8的中位数是![]()
C.要了解一批圆珠笔芯的使用寿命,应采用普查的方式
D.甲、乙两人各进行![]() 次射击,两人射击成绩的方差分别为
次射击,两人射击成绩的方差分别为![]() 则甲的射击成绩更稳定
则甲的射击成绩更稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com