
科目: 来源: 题型:
【题目】如图,AB是![]() 的直径,点E是
的直径,点E是![]() 的中点,CA与
的中点,CA与![]() 相切于点A交BE延长于点C,过点A作
相切于点A交BE延长于点C,过点A作![]() 于点F,交
于点F,交![]() 于点D,交BC于点Q,连接BD.
于点D,交BC于点Q,连接BD.
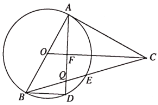
(1)求证:![]() ;
;
(2)若![]() ,求CQ的长.
,求CQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】国家卫生健康委员会公布,截止4月2日全国疫情现存趋势图如下:

(1)结合图象,小彤对全国疫情做出以下四个判断:
①现存疑似病例与现存确诊病例数量差距最大日期大约出现在2月上旬;
②疫情在3月30日已经得到完全的控制;
③现存疑似人数大约在2月8日前后达到峰值;
④全国现存确诊病例人数3月底增加趋缓.
你认为判断正确的有________.
(2)针对这次疫情,某校初三一班的同学以小组为单位组织了“抗战疫情,我为湖北鼓劲”绘画活动.通过网络发往湖北,右图是同学们的上交绘画作品情况,结合统计图,回答:![]() ________,
________,![]() ________.
________.

(3)全国各地都向湖北伸出援助之手,其中北京市派遣医务人员前往较为严重的武汉和黄冈.请依据表格回答下列问题:
北京派遣至武汉、黄冈各医院医护人员对比表 | ||||||
武汉 | ||||||
5 | 7 | 9 | 12 | 11 | 8 | 19 |
20 | 7 | 7 | 3 | 1 | 20 | 13 |
黄冈 | ||||||
3 | 8 | 5 | 10 | 14 | 20 | |
4 | 2 | 9 | 18 | 11 | 15 | |
注:表格内的数字代表派遣至每个医院的医护人员人数 | ||||||
①派往武汉各医院医护人员的众数是________人;
②派黄冈各医院医护人员的平均数约是________人(四舍五入取整数);
③请你根据表格信息,判断两个地区哪里的疫情较为严重,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,AC为一条对角线,且![]() .延长BC到点E,使
.延长BC到点E,使![]() ,连接DE.
,连接DE.
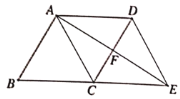
(1)判断四边形ACED的形状,并说明理由;
(2)连接AE交CD于点F,若![]() ,
,![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 中,
中,![]() ,M是BC的中点.如图.
,M是BC的中点.如图.
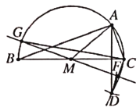
(1)以M为圆心.MB为半径,作半圆M﹔
(2)分别以B,C为圆心,BA,CA为半径作弧,两弧交于点D;
(3)连接AM,AD,CD;
(4)作线段CD的中垂线,分别交线段CD于点F,半圆M于点G,连接GC;
(5)以点G为圆心,线段GC为半径,作![]() .
.
根据以上作图过程及所作图形,下列结论中:
①点A在半圆M上;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() .一定正确的是________.
.一定正确的是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A坐标为![]() ,点B的坐标为
,点B的坐标为![]() .将二次函数
.将二次函数![]() 的图象经过左(右)平移
的图象经过左(右)平移![]() 个单位再上(下)平移
个单位再上(下)平移![]() 个单位得到图象M,使得图象M的顶点落在线段AB上.下列关于a,b的取值范围,叙述正确的是( )
个单位得到图象M,使得图象M的顶点落在线段AB上.下列关于a,b的取值范围,叙述正确的是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边
ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边![]() CDE.
CDE.
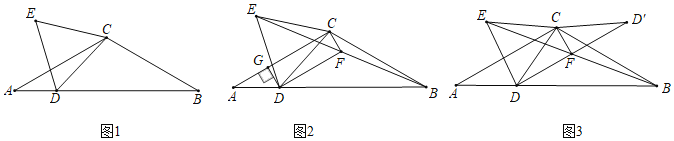
(1)如图1,若∠CDB=45°,AB=6,求等边![]() CDE的边长;
CDE的边长;
(2)如图2,点D在AB边上移动过程中,连接BE,取BE的中点F,连接CF,DF,过点D作DG⊥AC于点G.
①求证:CF⊥DF;
②如图3,将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,连接B
,连接B![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目: 来源: 题型:
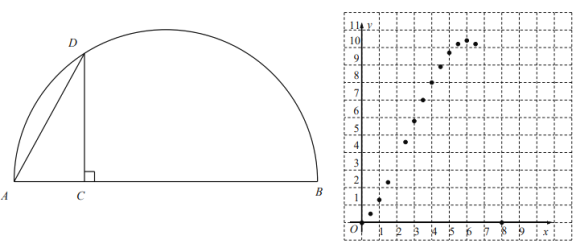
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com