
科目: 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目: 来源: 题型:
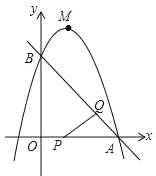
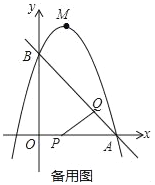
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
查看答案和解析>>
科目: 来源: 题型:
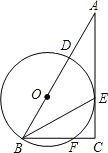
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
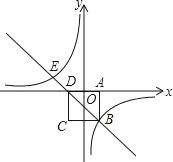
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
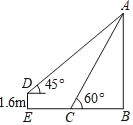
【题目】小明想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好在C处且与地面成60°角,小明拿起绳子末端,后退至E处,拉直绳子,此时绳子末端D距离地面1.6m且绳子与水平方向成45°角.
(1)填空:AD_____AC(填“>”,“<”,“=”).
(2)求旗杆AB的高度.
(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了了解九年级学生体育测试成绩情况,以九年级(1)班学生的体育测试成绩为样本,按B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分~74分;D级:60分以下)
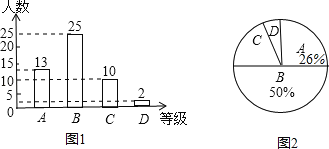
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图(图2)中C级所在的扇形圆心角的度数;
(3)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
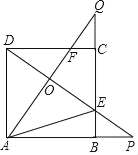
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com