
科目: 来源: 题型:
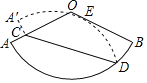
【题目】如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是![]() 上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=
上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD=45°,OC=![]() +1,则扇形AOB的半径长是( )
+1,则扇形AOB的半径长是( )
A. 2+![]() B. 2+
B. 2+![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
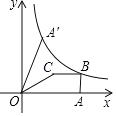
【题目】如图,平面直角坐标系xOy中,四边形OABC的边OA在x轴正半轴上,BC∥x轴,∠OAB=90°,点C(3,2),连接OC.以OC为对称轴将OA翻折到OA′,反比例函数y=![]() 的图象恰好经过点A′、B,则k的值是( )
的图象恰好经过点A′、B,则k的值是( )
A. 9B. ![]() C.
C. ![]() D. 3
D. 3![]()
查看答案和解析>>
科目: 来源: 题型:
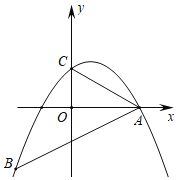
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
x2+bx+c的图象经过点A(4,0),B(﹣4,﹣4),且与y轴交于点C.
(1)求此二次函数的解析式;
(2)证明:AO平分∠BAC;
(3)在二次函数对称轴上是否存在一点P使得AP=BP?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、E在⊙O上,∠B=2∠ACE,在BA的延长线上有一点P,使得∠P=∠BAC,弦CE交AB于点F,连接AE.
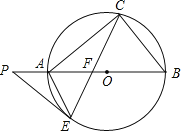
(1)求证:PE是⊙O的切线;
(2)若AF=2,AE=EF=![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目: 来源: 题型:
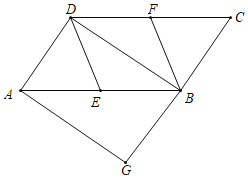
【题目】如图,在平行四边形ABCD中,点E、F分别为边AB、CD的中点,BD是平行四边形ABCD的对角线,AG∥BD交CB的延长线于点G
(1)求证:四边形BEDF是平行四边形;
(2)若AE=DE,则四边形AGBD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市农林种植专家指导贫困户种植红梨和青枣,收获的红梨和青枣优先进入该市水果市场.已知某水果经销商购进了红梨和青枣两种水果各10箱,分配给下属的甲、乙两个零售店(分别简称甲店、乙店)销售.预计每箱水果的盈利情况如表
红梨/箱 | 青枣/箱 | |
甲店 | 22元 | 34元 |
乙店 | 18元 | 26元 |
(1)若甲、乙两店各配货10箱,其中甲店配红梨2箱,青枣8箱;乙店配红梨8箱,青枣2箱,请你计算出经销商能盈利多少元?
(2)若甲、乙两店各配货10箱,且在保证乙店盈利不小于200元的条件下,请你设计出使水果经销商盈利最大的配货方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校文体艺术节期间,举办“爱我云南,唱我云南”文艺晚会.每个班推荐一个节目参加晩会表演,参加晚会表演的节目均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,明明根据获奖情况绘制岀如图所示的两幅统计图.请你根据图中所给信息解答下列问题.
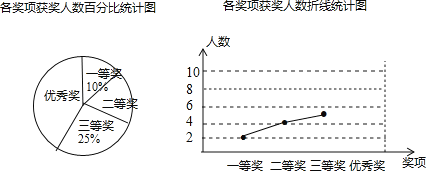
(1)二等奖的获奖人数所占的百分比是 ;
(2)在此次比赛中,一共有多少同学参赛?请将折线统计图补充完整.
查看答案和解析>>
科目: 来源: 题型:
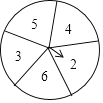
【题目】现有一个如图所示的标有2、3、4、5、6的转盘,另有五张分别标有1、2、3、4、5的扑克,小华和小亮用它们做游戏,先由小华转动转盘一次,记下指针停留时所指的数字;再由小亮随机抽取背面朝上的扑克一张,记下正面的数字.
(1)用列表法或画树状图的方法,求出记下的两个数字之和为8的概率.
(2)若记下的两个数字之和为奇数,则小华得1分;若记下的两个数字之和为偶数,则小亮得1分.这个游戏对双方公平吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BD为⊙O的直径,AC为⊙O的弦,AB=AC,AD交BC于点E,AE=2,ED=4,延长DB到点F,使得BF=BO,连接FA.则下列结论中不正确的是( )

A. △ABE∽△ADBB. ∠ABC=∠ADB
C. AB=3![]() D. 直线FA与⊙O相切
D. 直线FA与⊙O相切
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com