
科目: 来源: 题型:
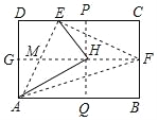
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE,再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF,已知HE=HF,下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
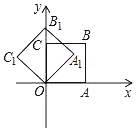
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2019次得到正方形OA2019B2019C2019,如果点A的坐标为(1,0),那么点B2019的坐标为( )
A. (1,1)B. ![]() C.
C. ![]() D. (﹣1,1)
D. (﹣1,1)
查看答案和解析>>
科目: 来源: 题型:
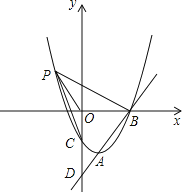
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目: 来源: 题型:
【题目】等腰Rt△ACB,∠ACB=90°,AC=BC,点A、C分别在x轴、y轴的正半轴上.

(1)如图1,求证:∠BCO=∠CAO
(2)如图2,若OA=5,OC=2,求B点的坐标
(3)如图3,点C(0,3),Q、A两点均在x轴上,且S△CQA=18.分别以AC、CQ为腰在第一、第二象限作等腰Rt△CAN、等腰Rt△QCM,连接MN交y轴于P点,OP的长度是否发生改变?若不变,求出OP的值;若变化,求OP的取值范围.
查看答案和解析>>
科目: 来源: 题型:
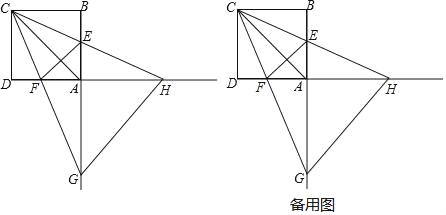
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目: 来源: 题型:
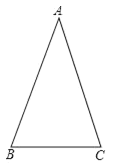
【题目】如图,△ABC中,AB=AC,∠A=36°.
(1)用尺规作图作∠ABC的角平分线,交AC于点D;(保留作图痕迹,不写作法).
(2)求证:△BCD是等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
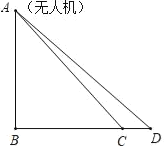
【题目】随着无人机的应用范围日益广泛,无人机已走进寻常百姓家,如图,小明在我市体训基地试飞无人机.为测量无人机飞行的高度AB,小明在C点处测得∠ACB=45°,向前走5米,到达D点处测得∠ADB=40°.求无人机飞行的高度AB.(参考数据:![]() ≈1.4,sin40°≈0.6,cos40°≈0.6,tan40°≈0.8.)
≈1.4,sin40°≈0.6,cos40°≈0.6,tan40°≈0.8.)
查看答案和解析>>
科目: 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com