
科目: 来源: 题型:
【题目】如图1,对角线互相垂直的四边形叫做垂美四边形.
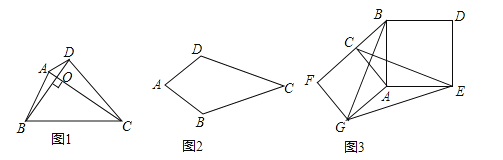
(1)概念理解:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,问四边形
,问四边形![]() 是垂美四边形吗?请说明理由;
是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形![]() 的对角线
的对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() .试证明:
.试证明:![]() ;
;
(3)解决问题:如图3,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() 、
、![]() 、
、![]() .已知
.已知![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目: 来源: 题型:
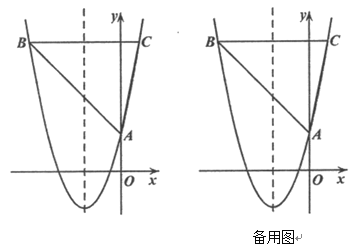
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,平行于
,平行于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在对称轴左侧,
在对称轴左侧,![]() .
.
I.求此抛物线的解析式;
Ⅱ.已知在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 的周长最小,求点
的周长最小,求点![]() 的坐标;
的坐标;
Ⅲ.若过点![]() 的直线
的直线![]() 将
将![]() 的面积分成2:3两部分,试求直线
的面积分成2:3两部分,试求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目: 来源: 题型:
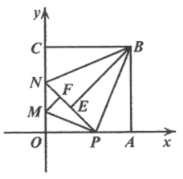
【题目】如图,在平面直角坐标系![]() 第一象限中有正方形
第一象限中有正方形![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点
轴上一动点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 落在点
落在点![]() 处。在
处。在![]() 上有一点
上有一点![]() ,使得将
,使得将![]() 沿直线
沿直线![]() 翻折后,点
翻折后,点![]() 落在直线
落在直线![]() 上的点
上的点![]() 处,直线
处,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
I.求证:![]() ;
;
Ⅱ.求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值;
的最大值;
Ⅲ.当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
I.请问1辆大货车和1辆小货车一次可以分别运货多少吨;
Ⅱ.目前有46.4吨货物需要运输,货运公司拟安排大小货车共10辆,全部货物一次运完.其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校组织全校1500名学生进行经典诗词诵背活动,为了解本次系列活动的效果,学校团委在活动开展一个月之后,随机抽取部分学生调查了“一周诗词诵背数量”,并根据调查结果绘制成如下的统计图1和图2.请根据相关信息,解答下列问题:
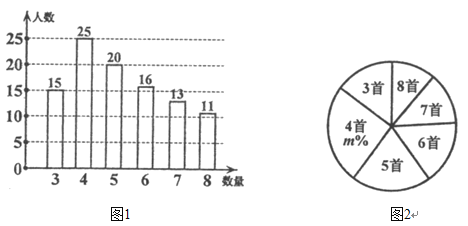
I.图2中的![]() 值为__________;
值为__________;
Ⅱ.求统计的这组数据的平均数、众数和中位数;
Ⅲ.估计此时该校学生一周诗词诵背6首(含6首)以上的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组![]() ;请结合题意填空,完成本题的解答。
;请结合题意填空,完成本题的解答。
I.解不等式①,得__________________;
Ⅱ.解不等式②,得__________________;
Ⅲ.把不等式①和②的解集在数轴上表示出来:

Ⅳ.原不等式组的解集为__________________.
查看答案和解析>>
科目: 来源: 题型:
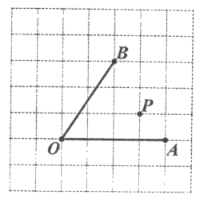
【题目】如图,在每个小正方形的边长为1的网格中,点![]() 、
、![]() 、
、![]() 、
、![]() 均在格点上.I.
均在格点上.I. ![]() 的长等于______________;Ⅱ.点
的长等于______________;Ⅱ.点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,当
上,当![]() 的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出
的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出![]() ,并简要说明点
,并简要说明点![]() ,
,![]() 的位置是如何找到的(不要求证明)____________ .
的位置是如何找到的(不要求证明)____________ .
查看答案和解析>>
科目: 来源: 题型:
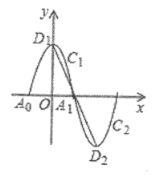
【题目】如图,一段抛物线![]() 为
为![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,顶点为
两点,顶点为![]() ;将
;将![]() 绕点
绕点![]() 旋转180°得到
旋转180°得到![]() ,顶点为
,顶点为![]() ;
;![]() 与
与![]() 组成一个新的图象.垂直于
组成一个新的图象.垂直于![]() 轴的直线
轴的直线![]() 与新图象交于点
与新图象交于点![]() ,
,![]() ,与线段
,与线段![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,
,![]() 均为正数,设
均为正数,设![]() ,则
,则![]() 的最大值是( )
的最大值是( )
A. 15B. 18C. 21D. 24
查看答案和解析>>
科目: 来源: 题型:
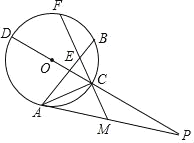
【题目】如图,CD是⊙O的直径,点A为圆上一点不与C,D点重合,过点A作⊙O的切线,与DC的延长线交于点P,点M为AP上一点,连接MC并延长,与⊙O交于点F,E为CF上一点,且MA=ME,连接AE并延长,与⊙O于点B,连接BC,AC.
(1)求证:![]() =
=![]() ;
;
(2)若PCPD=7,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com