
科目: 来源: 题型:
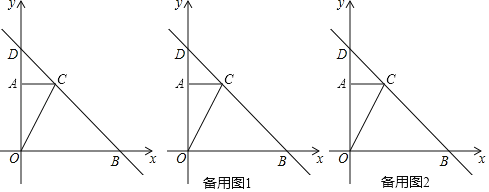
【题目】如图,在平面直角坐标系中,Rt△AOC的直角边OA在y轴正半轴上,且顶点O与坐标原点重合,点C的坐标为(1,2),直线y=﹣x+b过点C,与x轴交于点B,与y轴交于点D.
(1)B点的坐标为 ,D点的坐标为 ;
(2)动点P从点O出发,以每秒1个单位长度的速度,沿O→A→C的路线向点C运动,同时动点Q从点B出发,以相同速度沿BO的方向向点O运动,过点Q作QH⊥x轴,交线段BC或线段CO于点H.当点P到达点C时,点P和点Q都停止运动,在运动过程中,设动点P运动的时间为t秒:
①设△CPH的面积为S,求S关于t的函数关系式;
②是否存在以Q、P、H为顶点的三角形的面积与S相等?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
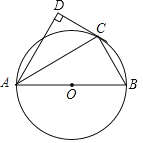
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
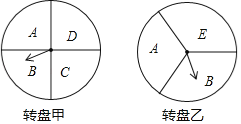
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为 ;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应国家的一带一路经济发展战略,树立品牌意识,我市质检部分别对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图:
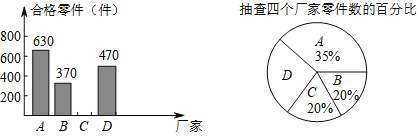
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 度;
(2)抽查C厂家的合格率零件为 件,并将图1补充完整;
(3)通过计算说明A、C两厂家谁的合格率更高?
查看答案和解析>>
科目: 来源: 题型:
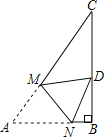
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=3,点M、N分别在线段AC、AB上,将△ANM沿直线M折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.
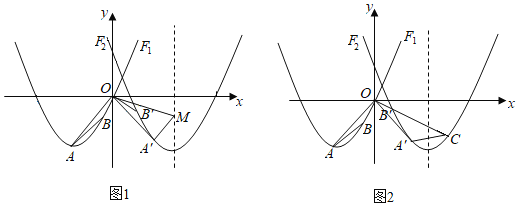
查看答案和解析>>
科目: 来源: 题型:
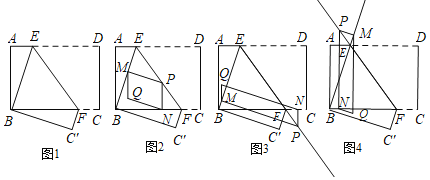
【题目】操作体验:如图,在矩形ABCD中,点E、F分别在边AD、BC上,将矩形ABCD沿直线EF折叠,使点D恰好与点B重合,点C落在点C′处.点P为直线EF上一动点(不与E、F重合),过点P分别作直线BE、BF的垂线,垂足分别为点M和N,以PM、PN为邻边构造平行四边形PMQN.
(1)如图1,求证:BE=BF;
(2)特例感知:如图2,若DE=5,CF=2,当点P在线段EF上运动时,求平行四边形PMQN的周长;
(3)类比探究:若DE=a,CF=b.
①如图3,当点P在线段EF的延长线上运动时,试用含a、b的式子表示QM与QN之间的数量关系,并证明;
②如图4,当点P在线段FE的延长线上运动时,请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】岳阳市整治农村“空心房”新模式,获评全国改革开放40年地方改革创新40案例.据了解,我市某地区对辖区内“空心房”进行整治,腾退土地1200亩用于复耕和改造,其中复耕土地面积比改造土地面积多600亩.
(1)求复耕土地和改造土地面积各为多少亩?
(2)该地区对需改造的土地进行合理规划,因地制宜建设若干花卉园和休闲小广场,要求休闲小广场总面积不超过花卉园总面积的![]() ,求休闲小广场总面积最多为多少亩?
,求休闲小广场总面积最多为多少亩?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O的直径,点P为AB延长线上的一点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE的垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是___________.(写出所有正确结论的序号)
①AM平分∠CAB;
②AM2=ACAB;
③若AB=4,∠APE=30°,则![]() 的长为
的长为![]() ;
;
④若AC=3,BD=1,则有CM=DM=![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
(1)表中m=__________,n=____________;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在_________分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com