
科目: 来源: 题型:
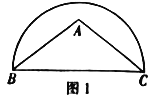
【题目】在![]() 中,
中,![]() ,点
,点![]() 在以
在以![]() 为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦![]() ,使
,使![]() ;
;
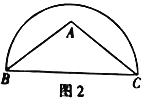
(2)在图2中以![]() 为边作一个45°的圆周角.
为边作一个45°的圆周角.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目: 来源: 题型:
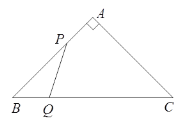
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0的两实数根为x1,x2,根据一元二次方程解的意义和因式分解法解一元二次方程可知,x1,x2也是(x﹣x1)(x﹣x2)=0的两个实数根,所以ax2+bx+c=a(x﹣x1)(x﹣x2).
利用这个结论可以解决一些相关问题.
(1)实数范围内因式分解:
例:分解因式2x2+2x﹣1
解:令2x2+2x﹣1=0,解这个方程,得
![]() =
=![]() .
.
即x1=![]() ,x2=
,x2=![]() .
.
所以 2x2+2x﹣1=![]() .
.
试仿照上例在实数范围内分解因式:x2﹣6x+1;
(2)解不等式:x2+2x﹣1>0;
(3)灵活运用:
已知方程(x﹣a)(x﹣b)﹣x=0的两个实数根是c、d,求方程(2x﹣c)(2x﹣d)+2x=0的根.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年人均收入人民币2600元,预计2018年人均收入将达到人民币13000元,设2016年到2018年该地区居民人均收入平均增长率为x,可列方程为( ).
A.2600(1+2x)=13000B.2600(1+x)2=13000
C.2600(1+x2)=13000D.2600+2x=13000
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)与
是常数)与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(Ⅰ)当![]() 时,求抛物线的解析式及顶点坐标;
时,求抛物线的解析式及顶点坐标;
(Ⅱ)在(Ⅰ)的条件下,![]() 为抛物线上的一个动点.
为抛物线上的一个动点.
①求当![]() 关于原点的对称点
关于原点的对称点![]() 落在直线
落在直线![]() 上时,求
上时,求![]() 的值;
的值;
②当![]() 关于原点的对称点
关于原点的对称点![]() 落在第一象限内,
落在第一象限内,![]() 取得最小值时,求
取得最小值时,求![]() 的值及这个最小值.
的值及这个最小值.
查看答案和解析>>
科目: 来源: 题型:
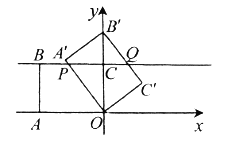
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
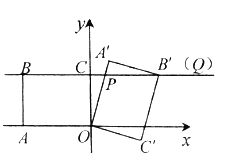
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有![]() 、
、![]() 型两种客车,它们的载客量和租金如下表:
型两种客车,它们的载客量和租金如下表:
|
| |
载客量/(人/辆) |
|
|
租金/(元/辆) |
|
|
某学校计划在总费用![]() 元的限额内,租用
元的限额内,租用![]() 、
、![]() 型客车共5辆送九年级师生集体外出活动.
型客车共5辆送九年级师生集体外出活动.
(Ⅰ)设租用![]() 型客车
型客车![]() 辆(
辆(![]() 为非负整数),根据题意,用含
为非负整数),根据题意,用含![]() 的式子填写下表:
的式子填写下表:
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
(Ⅱ)若九年级师生共有![]() 人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
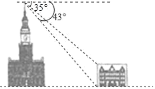
【题目】如图,甲、乙两座建筑物的水平距离BC为30m,从甲的顶部A处测得乙的顶部D处的俯角为35°测得底部C处的俯角为43°,求甲、乙两建筑物的高度AB和DC(结果取整数).
(参考数据:tan35°≈0.70,tan43°≈0.93)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com