
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点E、F分别在AC,AB上,连接EF.
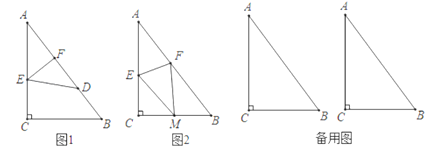
(1)将△ABC沿EF折叠,使点A落在AB边上的点D处,如图1,若S四边形ECBD=2S△EDF,求AE的长;
(2)将△ABC沿EF折叠,使点A落在BC边上的点M处,如图2,若MF⊥CB.
①求AE的长;②求四边形AEMF的面积;
(3)若点E在射线AC上,点F在边AB上,点A关于EF所在直线的对称点为点P,问:是否存在以PF、CB为对边的平行四边形,若存在,求出AE的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形![]() 中,
中,![]() 是
是![]() 中点,点
中点,点![]() 从点
从点![]() 出发沿
出发沿![]() 的路线匀速运动,到点
的路线匀速运动,到点![]() 停止,点
停止,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线匀速运动,
路线匀速运动,![]() 、
、![]() 两点同时出发,点
两点同时出发,点![]() 的速度是点
的速度是点![]() 速度的
速度的![]() 倍
倍![]() ,当点
,当点![]() 停止时,点
停止时,点![]() 也同时停止运动,设
也同时停止运动,设![]() 秒时,正方形
秒时,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
关于![]() 的函数关系如图2所示,则
的函数关系如图2所示,则
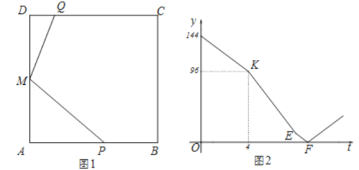
(1)求正方形边长![]() ;
;
(2)求![]() 的值;
的值;
(3)求图2中线段![]() 所在直线的解析式.
所在直线的解析式.
查看答案和解析>>
科目: 来源: 题型:
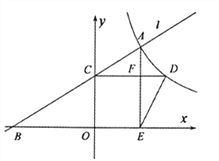
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
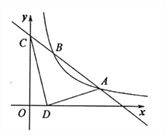
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式.
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品1件共需50元,购进甲商品1件和乙商品2件共需70元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件20元出售,乙商品以每件50元出售,为满足市场需求,需购进甲、乙两种商品共60件,若要保证获利不低于1000元,则甲商品最多能购进多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接![]() ,以
,以![]() 为长,
为长,![]() 为宽作矩形
为宽作矩形![]() ,且点
,且点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 也随之运动,但点
也随之运动,但点![]() 始终在反比例函数
始终在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com