
科目: 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( ).
A. AB∥DC,AD∥BCB. AB=DC,AD=BC
C. AO=CO,BO=DOD. AB∥DC,AD=BC
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
(1)如图,若△ABC为等边三角形,BM=1,CM=2,求AM的长;

小明在解决这个问题时采用的方法是:延长MC到E,使ME=AM,从而可证△AME为等边三角形,并且△ABM≌△ACE,进而就可求出线段AM的长.
请你借鉴小明的方法写出AM的长,并写出推理过程.
(2)若△ABC为等腰直角三角形,∠BAC=90°,![]() ,(其中b>a),直接写出AM的长(用含有a,b的代数式表示).
,(其中b>a),直接写出AM的长(用含有a,b的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:用配方法求最值.
已知x,y为非负实数,
∵x+y﹣![]()
∴x+y≥2![]() ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求y= x+![]() +4的最小值.
+4的最小值.
解:![]() +4=6
+4=6![]() ,当x=
,当x=![]() ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求y=![]() 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为![]() 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=![]()
![]() )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程x2+x-1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() .
.
把x=![]() 代入已知方程,得
代入已知方程,得![]() +
+![]() -1=0.
-1=0.
化简,得y2+2y-4=0.
故所求方程为y2+2y-4=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+x-2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为_________;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,在平面直角坐标系中,点 O 是坐标原点,四边形 ABCO 是菱形,点 A 的坐标为(-3,4),点 C 在 x 轴的正半轴上,直线 AC 交 y 轴于点 M,AB 边交 y 轴于点 H.
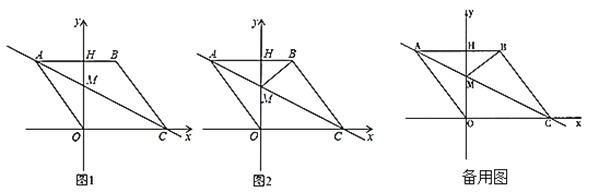
(1)求直线 AC 的解析式;
(2)连接 BM,如图 2,动点 P 从点 A 出发,沿折线 ABC 方向以 2 个单位/秒的速度向终点 C 匀速运动,设△PMB 的面积为 S(S≠0),点 P 的运动时间为 t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围);
(3)在(2)的条件下,当 t 为何值时,∠MPB 与∠BCO 互为余角,并求此时直线 OP 与直线 AC 所夹锐角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在四边形 ABCD 中,∠A+∠C=180°,DB 平分∠ADC.
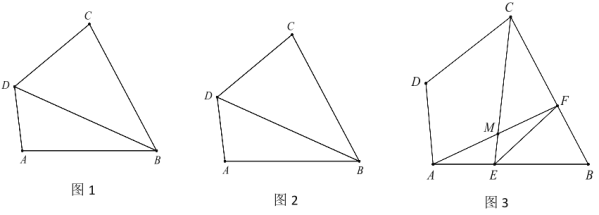
(1)如图 1求证:AB=BC
(2)如图 2,若∠ADB=60°,,试判断△ABC 的形状,并说明理由.
(3)如图 3,在(2)得条件下,在 AB 上取一点 E, BC 上取一点 F,连接 CE、AF 交于点 M,连接 EF,若∠CMF=60°,AD=EF=7,CD=8(CF﹥BF),求 AE 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店欲购进 A、B 两种商品,若购进 A 种商品 5 件和 B 种商品 4 件需 300 元;购进 A 种商品 6 件和 B 种商 品 8 件需 440 元.
(1)求 A、B 两种商品每件的进价分别为多少元?
(2)若该商店每销售 1 件 A 种商品可获利 8 元,每销售 1 件 B 种商品可获利 6 元,该商店准备购进 A、B 两种商 品共 50 件,且这两种商品全部售出后总获利超过 344 元,则至少购进多少件 A 商品?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com