
科目: 来源: 题型:
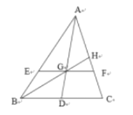
【题目】如图,已知在△ABC中,点D为BC边上一点(不与点B,点C重合),连结AD,点E、点F分别为AB、AC上的点,且EF∥BC,交AD于点G,连结BG,并延长BG交AC于点H.已知![]() =2,①若AD为BC边上的中线,
=2,①若AD为BC边上的中线,![]() 的值为
的值为![]() ;②若BH⊥AC,当BC>2CD时,
;②若BH⊥AC,当BC>2CD时,![]() <2sin∠DAC.则( )
<2sin∠DAC.则( )
A. ①正确;②不正确B. ①正确;②正确
C. ①不正确;②正确D. ①不正确;②正确
查看答案和解析>>
科目: 来源: 题型:
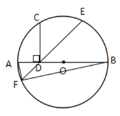
【题目】如图,AB是![]() 的直径,点D是半径OA的中点,过点D作CD⊥AB,交
的直径,点D是半径OA的中点,过点D作CD⊥AB,交![]() 于点C,点E为弧BC的中点,连结ED并延长ED交
于点C,点E为弧BC的中点,连结ED并延长ED交![]() 于点F,连结AF、BF,则( )
于点F,连结AF、BF,则( )
A. sin∠AFE=![]() B. cos∠BFE=
B. cos∠BFE=![]() C. tan∠EDB=
C. tan∠EDB=![]() D. tan∠BAF=
D. tan∠BAF=![]()
查看答案和解析>>
科目: 来源: 题型:
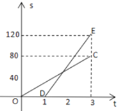
【题目】已知A,B两地相距120千米,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车,图中DE,OC分别表示甲、乙离开A地的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象,设在这个过程中,甲、乙两人相距y(单位:千米),则y关于t的函数图象是( )
A. 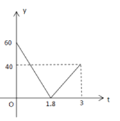 B.
B.  C.
C. 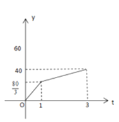 D.
D. 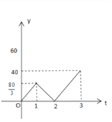
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2-4ax+b交x轴正半轴于A、B两点,交y轴正半轴于C,且OB=OC=3.
(1) 求抛物线的解析式;
(2) 如图1,D为抛物线的顶点,P为对称轴左侧抛物线上一点,连接OP交直线BC于G,连GD.是否存在点P,使![]() ?若存在,求点P的坐标;若不存在,请说明理由;
?若存在,求点P的坐标;若不存在,请说明理由;
(3) 如图2,将抛物线向上平移m个单位,交BC于点M、N.若∠MON=45°,求m的值.


查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD和四边形CEFG都是正方形,且AB>CE

(1) 如图1,连接BG、DE,求证:BG=DE
(2) 如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD
① 求∠BDE的度数
② 若正方形ABCD的边长是![]() ,请直接写出正方形CEFG的边长____________
,请直接写出正方形CEFG的边长____________
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件40元,售价每件不低于60元且每件不高于80元.当售价为每件60元是,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当每件商品定价为多少元使得每个月的利润恰为2250元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.

(1)求出y与x的函数关系式。
(2)当矩形花圃的面积为48m2时,求x的值。
(3)当边长x为多少时,矩形的面积最大,最大面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),说法:① abc<0;② 2a-b=0;③ 4a-2b+c<0;④ 若(-5,y1)、(![]() ,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个
,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个
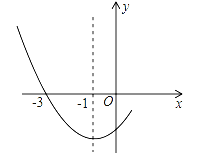
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
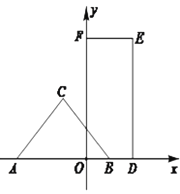
【题目】如图,等腰直角![]() 的斜边
的斜边![]() 在x轴上且长为4,点C在x轴上方.矩形
在x轴上且长为4,点C在x轴上方.矩形![]() 中,点D、F分别落在x、y轴上,边
中,点D、F分别落在x、y轴上,边![]() 长为2,
长为2,![]() 长为4,将等腰直角
长为4,将等腰直角![]() 沿x轴向右平移得等腰直角
沿x轴向右平移得等腰直角![]() .
.
(1)当点![]() 与点D重合时,求直线
与点D重合时,求直线![]() 的解析式;
的解析式;
(2)连接![]() ,
,![]() .当线段
.当线段![]() 和线段
和线段![]() 之和最短时,求矩形
之和最短时,求矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积;
重叠部分的面积;
(3)当矩形![]() 和等腰直角
和等腰直角![]() 重叠部分的面积为
重叠部分的面积为![]() 时,求直线
时,求直线![]() 与y轴交点的坐标.(本问直接写出答案即可)
与y轴交点的坐标.(本问直接写出答案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com