
科目: 来源: 题型:
【题目】如图,直线y=-![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
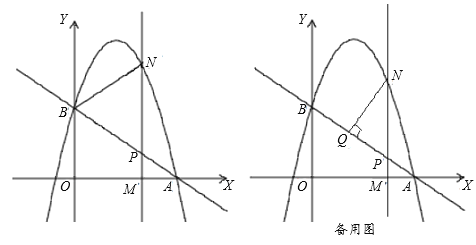
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若△BPN∽△APM,求点M的坐标;
②过点N作NQ⊥AB于Q,当N点坐标是多少时,NQ取得最大值,最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P, AC=PC,∠COB=2∠PCB.

(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,与反比例函数的图象交于点C,连接CO,过C作CD⊥x轴于D,已知tan∠ABO=![]() ,OB=4,OD=2.
,OB=4,OD=2.
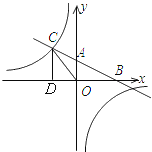
(1)求直线AB和反比例函数的解析式;
(2)在x轴上有一点E,使△CDE与△COB的面积相等,求点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A是我市某小学,在位于学校南偏西15°方向距离120米的C点处有一消防车.某一时刻消防车突然接到报警电话,告知在位于C点北偏东75°方向的F点处突发火灾,消防队必须立即沿路线CF赶往救火.已知消防车的警报声传播半径为110米,问消防车的警报声对学校是否会造成影响?若会造成影响,已知消防车行驶的速度为每小时60千米,则对学校的影响时间为几秒?(![]() ≈3.6,结果精确到1秒)
≈3.6,结果精确到1秒)
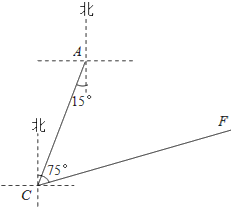
查看答案和解析>>
科目: 来源: 题型:
【题目】现有一段120m的篱笆,准备用这些篱笆借助一段墙角围成如图所示两块面积相同的矩形场地养鸡.
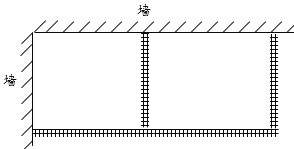
(1)如图所示,若围成的场地总面积为1750m2,则该场地的宽(图中纵向)应为多少?
(2)能不能围成面积为2000m2的场地?若能,求出此时篱笆的宽;若不能,求围成场地面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①abc>0;②4a+b=0;③若点B(﹣3,y1)、C(﹣4,y2)为函数图象上的两点,则y2<y1;④a+b+c=0.其中,正确结论的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
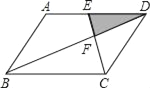
A. 8S B. 9S C. 10S D. 11S
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+2的图象与x轴相交于点A(﹣1,0)、B(4,0),与y轴相交于点C.

(1)求该函数的表达式;
(2)点P为该函数在第一象限内的图象上一点,过点P作PQ⊥BC,垂足为点Q,连接PC.
①求线段PQ的最大值;
②若以点P、C、Q为顶点的三角形与△ABC相似,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
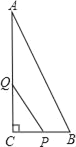
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场经营某种品牌的童装,购进时的单价是![]() 元.根据市场调查,在一段时间内,销售单价是
元.根据市场调查,在一段时间内,销售单价是![]() 元时,销售量是
元时,销售量是![]() 件.而销售单价每降低
件.而销售单价每降低![]() 元,就可多售出
元,就可多售出![]() 件.
件.
![]() 求出销售该品牌童装获得的利润
求出销售该品牌童装获得的利润![]() 元与销售单价
元与销售单价![]() 元之间的函数关系式;
元之间的函数关系式;
![]() 若童装厂规定该品牌童装销售单价不低于
若童装厂规定该品牌童装销售单价不低于![]() 元,且商场要完成不少于
元,且商场要完成不少于![]() 件的销售
件的销售
任务,则商场销售该品牌童装获得的最大利润是多少元?
![]() 如果要使利润不低于
如果要使利润不低于![]() 元,那么销售单价应在什么取值范围内?
元,那么销售单价应在什么取值范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com