
科目: 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边的长.
(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目: 来源: 题型:
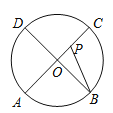
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. 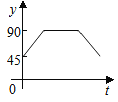 B.
B. 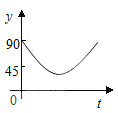 C.
C. 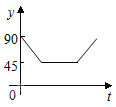 D.
D. 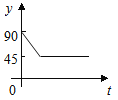
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
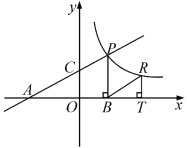
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目: 来源: 题型:
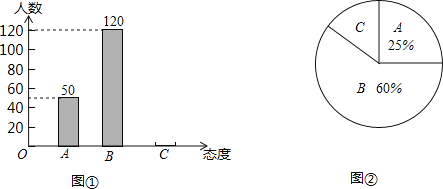
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中.共调査了 名中学生家长;
(2)将图①补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2经过点A(2,1).
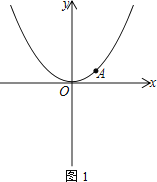
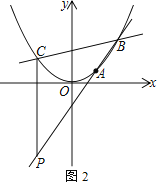
(1) 求a的值;
(2) 如图1,点M为x轴负半轴上一点,线段AM交抛物线于N.若△OMN为等腰三角形,求点N的坐标;
(3) 如图2,直线y=kx-2k+3交抛物线于B、C两点,过点C作CP⊥x轴,交直线AB于点P,请说明点P一定在某条确定的直线上运动,求出这条直线的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】四边形ABCD中,AB=BC,∠B=∠C=90°,P是BC边上一点,AP⊥PD,E是AB边上一点,∠BPE=∠BAP.
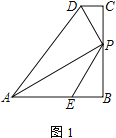
(1) 如图1,若AE=PE,直接写出![]() =______;
=______;
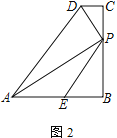
(2) 如图2,求证:AP=PD+PE;
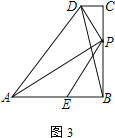
(3) 如图3,当AE=BP时,连BD,则![]() =______,并说明理由.
=______,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一张长10 dm,宽6 dm矩形纸板,将纸板四个角各剪去一个同样的边长为x dm的正方形,然后将四周突出部分折起,可制成一个无盖方盒.
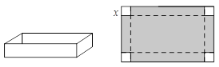
(1) 无盖方盒盒底的长为______dm,宽为_____dm(用含x的式子表示)
(2) 若要制作一个底面积是32dm2的一个无盖长方体纸盒,求剪去的正方形边长x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com