
科目: 来源: 题型:
【题目】数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
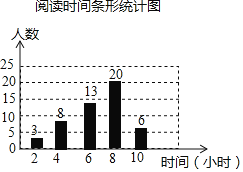
A.中位数和众数都是8小时B.中位数是25人,众数是20人
C.中位数是13人,众数是20人D.中位数是6小时,众数是8小时
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 经过点E(5,5),其顶点为C点.
经过点E(5,5),其顶点为C点.
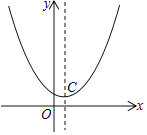
(1)求抛物线的解析式,并直接写出C点坐标.
(2)将直线![]() 沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
沿y轴向上平移b个单位长度交抛物线于A、B两点.若∠ACB=90°,求b的值.
(3)是否存在点D(1,a),使抛物线上任意一点P到x轴的距离等于P点到点D的距离?若存在,请求点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】超市里,某商户先后两次购进若干千克的黄瓜,第一次用了300元,第二次用了900元,但第二次的进货单价比第次的要高1.5元,而所购的黄瓜数量是第一次的2倍.
(1)问该商户两次一共购进了多少千克黄瓜?
(2)当商户按每千克6元的价格卖掉了![]() 时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
时,商户想尽快卖掉这些黄瓜,于是商户决定将剩余的黄瓜打折销售,请你帮忙算算,剩余的黄瓜至少打几折才能使两次所进的黄瓜总盈利不低于360元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了“频率分布直方图”(如图).请回答:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)这次竞赛成绩的中位数落在哪个分数段内?
(4)图中还提供了其它信息,例如该中学没有获得满分的同学等等,请再写出两条信息.
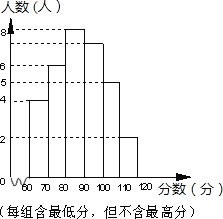
查看答案和解析>>
科目: 来源: 题型:
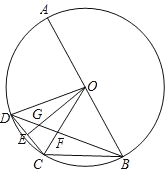
【题目】如图,AB是⊙O的直径,弦BC=OB,点D是![]() 上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
上一动点,点E是CD中点,连接BD分别交OC,OE于点F,G.
(1)求∠DGE的度数;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)记△CFB,△DGO的面积分别为S1,S2,若![]() =k,求
=k,求![]() 的值.(用含k的式子表示)
的值.(用含k的式子表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和直线m,给出如下定义:若存在一点P,使得点P到直线m的距离等于1,则称P为直线m的平行点.
(1)当直线m的表达式为y=x时,
①在点![]() ,
,![]() ,
,![]() 中,直线m的平行点是______;
中,直线m的平行点是______;
②⊙O的半径为![]() ,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
,点Q在⊙O上,若点Q为直线m的平行点,求点Q的坐标.
(2)点A的坐标为(n,0),⊙A半径等于1,若⊙A上存在直线![]() 的平行点,直接写出n的取值范围.
的平行点,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
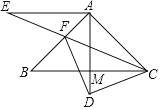
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,M是BC的中点,延长AM到点D,AE=AD,∠EAD=90°,CE交AB于点F,CD=DF.
(1)∠CAD=______度;
(2)求∠CDF的度数;
(3)用等式表示线段CD和CE之间的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
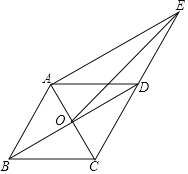
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)连接OE,若∠ABC=60°,且AD=DE=4,求OE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:如图2,
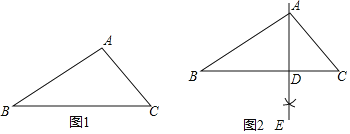
(1)分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点E;
(2)作直线AE交BC边于点D.所以线段AD就是所求作的高.
请回答:该尺规作图的依据是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com