
科目: 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>3,其中正确的个数是
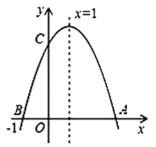
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
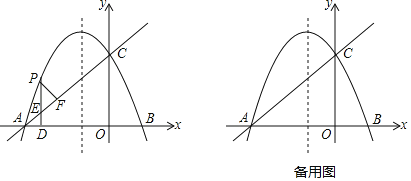
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D,E,N分别是△ABC的AB,AC,BC边上的中点,连接AN,DE交于点M.
(1)观察猜想:![]() 的值为 :
的值为 :![]() 的值为 ;
的值为 ;
(2)探究与证明:将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM随之旋转,如图2所示,连接BD,CE,MN,试探究线段BD与CE和BD与MN之间分别有什么样的数量关系,并证明;
(3)拓展与延伸:△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,BF= .
查看答案和解析>>
科目: 来源: 题型:
【题目】为了美化城市环境,某街道重修了路面,准备将老旧的路灯换成LED太阳能路灯,计划购买海螺臂和A字臂两种型号的太阳能路灯共100只,经过市场调查:购买海螺臂太阳能路灯1只,A字臂太阳能路灯2只共需2300元;购买海螺臂太阳能路灯3只,A字臂太阳能路灯4只共需5400元.

(1)求海螺臂太阳能路灯和A字臂太阳能路灯的单价:
(2)在实际购买时,恰逢商家活动,购买海螺臂太阳能路灯超过20只时,超过的部分打九折优惠,A字臂太阳能路灯全部打八折优惠;若规定购买的海螺臂太阳能路灯的数量不少于A字臂太阳能路灯的数量的一半,请你设计一种购买方案,使得总费用最少,并求出最小总费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘渔船位于灯塔A的南偏西75°方向的B处,距离A处30海里,渔船沿北偏东30°方向追寻鱼群,航行一段时间后,到达位于A处北偏西20°方向的C处,渔船出现了故障立即向正在灯塔A处的巡逻船发出求救信号.巡逻船收到信号后以40海里每小时的速度前往救助,请问巡逻船多少分钟能够到达C处?(参考数据:![]() ≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
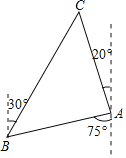
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知将反比例函数![]() (x<0),沿y轴翻折得到反比例函数
(x<0),沿y轴翻折得到反比例函数![]() (x>0),一次函数y=ax+b与
(x>0),一次函数y=ax+b与![]() 交于A(1,m),B(4,n)两点;
交于A(1,m),B(4,n)两点;
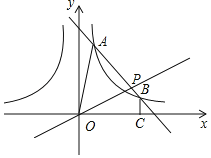
(1)求反比例函数y2和一次函数y=ax+b的解析式;
(2)连接OA,过B作BC⊥x轴,垂足为C,点P是线段AB上一点,若直线OP将四边形OABC的面积分成1:2两部分,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,C是半圆O上一个动点,AB为半圆的直径,D是弧BC的中点,过点D作半圆O的切线DE交AC的延长线于点E.
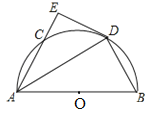
(1)求证:AE⊥DE;
(2)①已知CE=2,DE=4,则AB= ;
②连接OC,DC,当∠BAC= 度时,四边形OBDC为菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】近日,全省各地市的2019年初中毕业升学体育考试工作正依照某省教育厅的具体要求在有条不紊的进行当中,某中学在正式考试前,为了让同学们在中招体育考试中获得理想成绩,同时为了了解学生的当前水平,按批次进行了模拟考试,并随机抽取若干名学生问卷调查,现将调查结果绘制成如下不完整的统计图表:
组别 | 成绩范围x(分) | 频数(人数) |
A | 60<x≤70 | 54 |
B | 50<x≤60 | m |
C | 40<x≤50 | n |
D | 30<x≤40 | 6 |
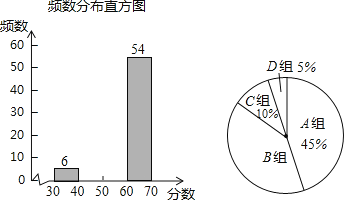
(1)这次调查的总人数有 人,表中的m= ,n= ;
(2)扇形统计图中B组对应的圆心角为 °;
(3)请补全频数分布直方图;
(4)若该校九年级共有学生2700名,且都参加了正式的初中毕业升学体育考试,小华也参加了这次考试并得了67分,若规定60分以上为优秀,体育老师想要在获得优秀的学生中随机抽出1名,作为学生代表向学弟学妹们传授经验,求抽到小华的概率.
查看答案和解析>>
科目: 来源: 题型:
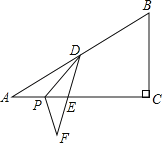
【题目】如图,在Rt△ABC中,∠C=90°,BC=2,∠A=30°,点D是AB的中点,P是AC边上一动点,连接DP,将△DPA沿着DP折叠,A点落到F处,DF与AC交于点E,当△DPF的一边与BC平行时,线段DE的长为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若BF=3,AB=2.5,则AE的长为( )
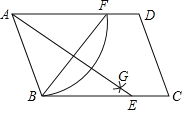
A.2B.4C.8D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com