它们是按一定规律排列的，依照此规律，第5个图形中的五角星的个数为___，第n个图形中的五角星(n为正整数)个数为____(用含n的代数式表示)．

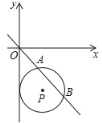
【题目】如图，在平面直角坐标系中，⊙P的圆心是（2，a），半径为2，直线y＝﹣x与⊙P相交于A、B两点，若弦AB的长为2，则a的值是（　　）

A. ﹣2B. ﹣2+C. ﹣2﹣D. ﹣2﹣

（1）求抛物线的解析式；

（2）以线段EH为斜边向右作等腰直角△EHG，当点G落在第一象限内的抛物线上时，求出t的值；

（3）设△EFM与四边形ADCB重合时的面积为S，请直接写出S与t的函数关系式与相应的自变量t的取值范围．

（1）求证：AE是⊙O的切线；

（2）若，AE=8，求⊙O的半径；

（3）在(2)条件下，求BF的长。

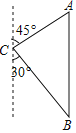
【题目】如图，一艘海轮位于灯塔C的北偏东45方向，距离灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔C的南偏东30°方向上的B处，求此时船距灯塔的距离（参考数据：≈1.414，≈1.732，结果取整数）．

【题目】某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量（万件）与销售单价（元）之间的关系可以近似地看作一次函数（利润=售价﹣制造成本）

（1）写出每月的利润（万元）与销售单价（元）之间的函数关系式；

（2）根据相关部门规定，这种电子产品的销售单价不能高于40元，如果厂商每月的制造成本不超过540万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？

（1）此次抽查的学生数为　 　人，并补全条形统计图；

（2）从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是　　　　；

（3）若当天在校学生数为1200人，请估计在当天达到国家规定体育活动时间的学生有　　人．

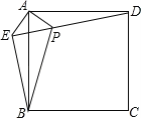
【题目】如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD+S△APB=1+；⑤S正方形ABCD=4+．其中正确结论的序号是 ．

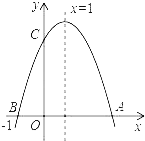
A.①②④B.②④C.①④D.②③

如图1，四边形ABCD中，AB＝BC，∠B+∠D＝180°（或∠A+∠C＝180°），则四边形ABCD叫做“邻等对补四边形”．

概念理解

（1）在以下四种图形中：①平行四边形，②菱形，③矩形，④正方形；一定是“邻等对补四边形”的是　 　；（填写序号）

（2）如图2，点A、B、C是网格中格点，请找出两个格点P1，P2，连接P1A、P1C，P2A、P2C画出四边形P1ABC，P2ABC，使四边形P1ABC，P2ABC均为“邻等对补四边形”．

性质证明

（3）如图1，四边形ABCD中，AB＝BC，∠A+∠C＝180°，连接BD，求证：BD平分∠ADC．

知识运用

（4）如图3，在“邻等对补四边形”ABCD中，满足AB＝AD，AB+BC＝6，∠ADC＝60°时，若2≤BC＜3，求四边形ABCD的面积的最大值．