
科目: 来源: 题型:
【题目】某超市销售一种商品,每件的成本每千克18元,规定每千克售价不低于成本,且获利不得高于100%,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 39 | 38 | 37 |
销售量y(千克) | 20 | 22 | 24 | 26 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
(3)该超市若想每天销售利润不低于480元,请结合函数图象帮助超市确定产品的销售单价范围?
查看答案和解析>>
科目: 来源: 题型:
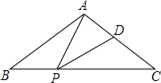
【题目】如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:△ABP∽△PCD;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为
,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为![]() ,则其升高可能是( )
,则其升高可能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
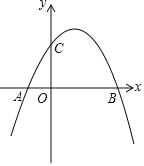
【题目】如图,抛物线 y=﹣![]() x2+
x2+![]() x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
x+2 与 x 轴交于点 A,B,与 y 轴交于点C.
(1)求 A,B,C的坐标;
(2)直线 l:y=﹣![]() x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
x+2上有一点 D(m,﹣2),在图中画出直线 l和点 D,并判断四边形ACBD的形状,说明理由.
查看答案和解析>>
科目: 来源: 题型:
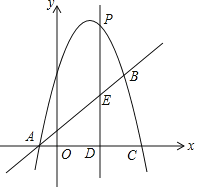
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P是抛物线上的一个动点
点P是抛物线上的一个动点![]() 不与点A、点B重合
不与点A、点B重合![]() ,过点P作直线
,过点P作直线![]() 轴于点D,交直线AB于点E.
轴于点D,交直线AB于点E.
![]() 当
当![]() 时,求P点坐标;
时,求P点坐标;
![]() 是否存在点P使
是否存在点P使![]() 为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1矩形ABCD中,点E是CD边上的动点(点E不与点C,D重合),连接AE,过点A作AF⊥AE交CB延长线于点F,连接EF,点G为EF的中点,连接BG.
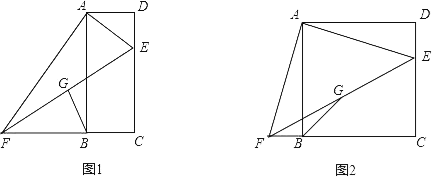
(1)求证:△ADE∽△ABF;
(2)若AB=20,AD=10,设DE=x,点G到直线BC的距离为y.
①求y与x的函数关系式;②当![]() 时,x的值为 ;
时,x的值为 ;
(3)如图2,若AB=BC,设四边形ABCD的面积为S,四边形BCEG的面积为S1,当![]() 时,DE:DC的值为 .
时,DE:DC的值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】创客联盟的队员想用3D的打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如表:
材料 | 甲 | 乙 |
价格(元/米2) | 50 | 40 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
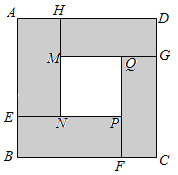
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备资金1700元购买材料一定够用吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读理解)对于任意正实数a、b,
∵![]() ≥0,
≥0,
∴a﹣2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b=2
,(只有当a=b时,a+b=2![]() ).
).
即当a=b时,a+b取得最小值,且最小值为2![]() .
.
根据上述内容,回答下列问题:
问题1:若m>0,当m= 时,m+![]() 有最小值为 ;
有最小值为 ;
问题2:若函数y=a+![]() ,则当a= 时,函数y=a+
,则当a= 时,函数y=a+![]() 有最小值为 ;
有最小值为 ;
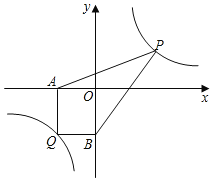
(探索应用)已知点Q(﹣3,﹣4)是双曲线y=![]() 上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q做QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() 上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com