
科目: 来源: 题型:
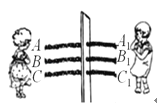
【题目】如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
(1)问:“姐妹两人同时选中同一根绳子”这一事件是 事件,概率是 ;
(2)在互相看不见的条件下,姐姐先将左侧A、C两个绳端打成一个连结,则妹妹从右侧A1、B1、C1三个绳端中随机选两个打一个结(打结后仍能自由地通过木孔);请求出“姐姐抽动绳端B,能抽出由三根绳子连结成一根长绳”的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
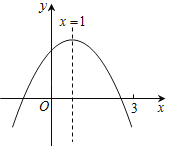
A.①②③B.②④C.②⑤D.②③⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
,称为黄金比例),如图,著名的“断臂维纳斯”便是如此,此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() ,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为
,若某人的身材满足上述两个黄金比例,且头顶至咽喉的长度为![]() ,则其升高可能是( )
,则其升高可能是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()

A.50°B.60°C.70°D.80°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
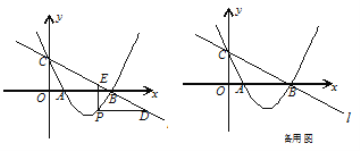
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
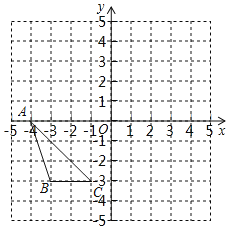
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个顶点的坐标分别为A(﹣4,0),B(﹣3,﹣3),C(﹣1,﹣3).
(1)画出△ABC关于x轴对称的△ADE(其中点B,C的对称点分别为点D、E);
(2)画出△ABC关于原点成中心对称的△FGH(其中A、B、C的对称点分别为点F,G,H).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
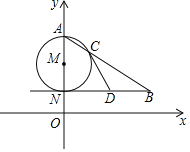
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com