
科目: 来源: 题型:
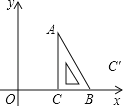
【题目】如图,把一块含有30°角的直角三角尺放置在平面直角坐标系中,BC边落在x轴的正半轴上,点A在第一象限内,∠ACB=90°,∠CAB=30°,AC=4![]() ,沿着AB翻折三角尺,直角顶点C落在C′处.设A、C′两点的横坐标分别为m、n.
,沿着AB翻折三角尺,直角顶点C落在C′处.设A、C′两点的横坐标分别为m、n.
(1)试用m的代数式表示n;
(2)若反比例函数y=![]() (x>0)的图象恰好经过A、C′两点,求k的值.
(x>0)的图象恰好经过A、C′两点,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
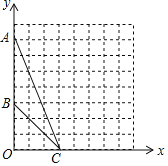
(1)在图中作出△ABC的外接圆⊙P(保留必要的作图痕迹,不写作法)
(2) 若在x轴的正半轴上有一点D(异与C点),且∠ADB=∠ACB,则点D的坐标为 .
(3)若用扇形PAC围成一个圆锥,那么这个圆锥的底面半径为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目: 来源: 题型:
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
查看答案和解析>>
科目: 来源: 题型:
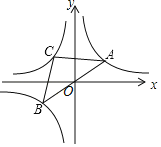
【题目】如图,已知A,B为反比例函数y1=![]() 图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=
图象上两点,连接AB,线段AB经过点O,C是反比例函数y2=![]() (k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且
(k<0)在第二象限内的图象上一点,当△CAB是以AB为底的等腰三角形,且![]() 时,k的值为( )
时,k的值为( )
A.﹣![]() B.﹣3C.﹣4D.﹣
B.﹣3C.﹣4D.﹣![]()
查看答案和解析>>
科目: 来源: 题型:
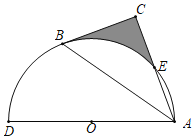
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E;B、E是半圆弧的三等分点,![]() 的长为
的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠D=∠B,补充下列条件之一,不一定能判定△ABC和△ADE相似的是( )
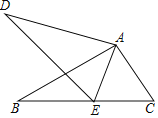
A.∠ACB=∠AEDB.∠CAE=∠BADC.∠BED=∠EACD.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
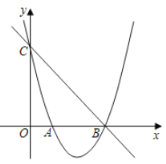
(1)求此抛物线的解析式;
(2)若点![]() 是直线
是直线![]() 下方的抛物线上一动点(不点
下方的抛物线上一动点(不点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
②连接![]() ,
,![]() ,求
,求![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 是抛物线的对称轴上一点,
是抛物线的对称轴上一点,![]() 为
为![]() 轴上一点,是否存在这样的点
轴上一点,是否存在这样的点![]() 和点
和点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?如果存在,请直接写出点
为顶点的四边形是菱形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
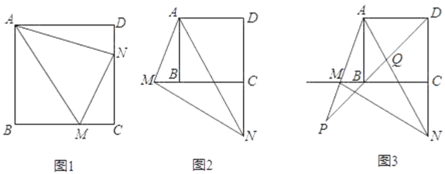
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com