
科目: 来源: 题型:
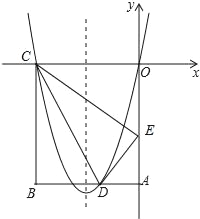
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求点E坐标及经过O,D,C三点的抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,OA=3,OC=4,P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90交直线BC于点Q.
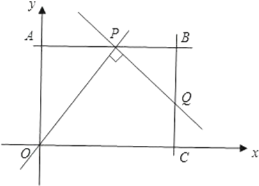
(1)当点P在线段AB上运动(不与A,B重合)时,求证:OABQ=APBP;
(2)在(1)成立的条件下,设点P的横坐标为m,线段CQ的长度为![]() ,求出
,求出![]() 关于m的函数解析式,并判断
关于m的函数解析式,并判断![]() 是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
是否存在最小值?若存在,请求出最小值;若不存在,请说明理由;
(3)直线AB上是否存在点P,使△POQ为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
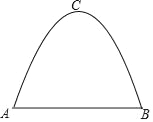
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目: 来源: 题型:
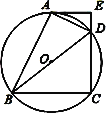
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点C的坐标为(
),点C的坐标为(![]() ,
,![]() ).
).
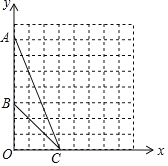
(1)在图中作出![]() 的外接圆(利用格图确定圆心);
的外接圆(利用格图确定圆心);
(2)圆心坐标为 _____;外接圆半径![]() 为 _____;
为 _____;
(3)若在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.
查看答案和解析>>
科目: 来源: 题型:
【题目】九年级某班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组数据的中位数是________,乙组数据的众数是________;
(2)已知甲组数据的方差是1.4分2 ,则成绩较为整齐的是哪个队?
查看答案和解析>>
科目: 来源: 题型:
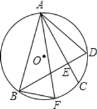
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com