
科目: 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
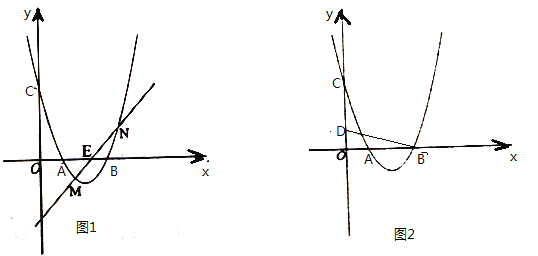
(1)填空:![]() ,
,![]() .
.
(2)如图1,已知![]() ,过点
,过点![]() 的直线与抛物线交于点
的直线与抛物线交于点![]() 、
、![]() ,且点
,且点![]() 、
、![]() 关于点
关于点![]() 对称,求直线
对称,求直线![]() 的解析式.
的解析式.
(3)如图2,已知![]() ,
,![]() 是第一象限内抛物线上一点,作
是第一象限内抛物线上一点,作![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 相似,请求出点
相似,请求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,
,![]() .
.
(1)如图1,求![]() 的值.
的值.
(2)把![]() 绕着点
绕着点![]() 顺时针旋转,点
顺时针旋转,点![]() 、
、![]() 旋转后对应的点分别为
旋转后对应的点分别为![]() 、
、![]() .
.
①当![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求出点
的延长线上时,如图2,求出点![]() 、
、![]() 的坐标.
的坐标.
②若点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点,如图3,在旋转过程中,请直接写出线段
上的动点,如图3,在旋转过程中,请直接写出线段![]() 长的取值范围.
长的取值范围.
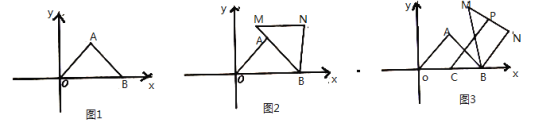
查看答案和解析>>
科目: 来源: 题型:
【题目】采用东阳南枣通过古法熬制而成的蜜枣是我们东阳的土特产之一,已知蜜枣每袋成本10元.试销后发现每袋的销售价![]() (元)与日销售量
(元)与日销售量![]() (袋)之间的关系如下表:
(袋)之间的关系如下表:
| 15 | 20 | 30 | … |
| 25 | 20 | 10 | … |
若日销售量![]() 是销售价
是销售价![]() 的一次函数,试求:
的一次函数,试求:
(1)日销售量![]() (袋)与销售价
(袋)与销售价![]() (元)的函数关系式.
(元)的函数关系式.
(2)要使这种蜜枣每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是小区常见的漫步机,从侧面看如图2,踏板静止时,踏板连杆与立柱![]() 上的线段
上的线段![]() 重合,
重合,![]() 长为0.2米,当踏板连杆绕着点
长为0.2米,当踏板连杆绕着点![]() 旋转到
旋转到![]() 处时,测得
处时,测得![]() ,此时点
,此时点![]() 距离地面的高度
距离地面的高度![]() 为0.44米.求:
为0.44米.求:

(1)踏板连杆![]() 的长.
的长.
(2)此时点![]() 到立柱
到立柱![]() 的距离.(参考数据:
的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在综合实践课中,小慧将一张长方形卡纸如图1所示裁剪开,无缝隙不重叠的拼成如图2所示的“![]() ”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知
”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知![]() ,
,![]() ,
,![]() .
.
求(1)线段![]() 与
与![]() 的差值是___
的差值是___
(2)![]() 的长度.
的长度.
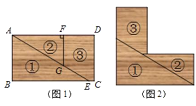
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系中,四边形ABCO是菱形,点C的坐标为(﹣3,4),点A在x轴的正半轴上,O为坐标原点,连接OB,抛物线y=ax2+bx+c经过C、O、A三点.
(1)直接写出这条抛物线的解析式;
(2)如图1,对于所求抛物线对称轴上的一点E,设△EBO的面积为S1,菱形ABCO的面积为S2,当S1≤![]() S2时,求点E的纵坐标n的取值范围;
S2时,求点E的纵坐标n的取值范围;
(3)如图2,D(0,﹣![]() )为y轴上一点,连接AD,动点P从点O出发,以
)为y轴上一点,连接AD,动点P从点O出发,以![]() 个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B方向运动,设点P运动时间为t秒(0<t≤6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.
个单位/秒的速度沿OB方向运动,1秒后,动点Q从O出发,以2个单位/秒的速度沿折线O﹣A﹣B方向运动,设点P运动时间为t秒(0<t≤6),是否存在实数t,使得以P、Q、B为顶点的三角形与△ADO相似?若存在,求出相应的t值;若不存在,请说明理由.
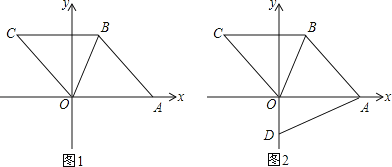
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com