
科目: 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
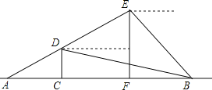
(1)分别求隧道AC和BC段的长度;
(2)建工集团安排甲、乙两个金牌施工队分别从隧道两头向中间施工,甲队负责AC段施工,乙队负责BC段施工,乙每天的工作量是甲的2倍,两队同时开工5天后,甲队将速度提高25%,乙队将速度提高了150%,从而两队同时完成,求原计划甲、乙两队每天各施工多少米.(参考数据:tan23°≈0.4,cos23°≈0.9)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线11:y1=kx+b与反比例函数y2=![]() 相交于A(﹣1,4)和B(﹣4,a),直线12:y3=﹣x+e与反比例函数y2=
相交于A(﹣1,4)和B(﹣4,a),直线12:y3=﹣x+e与反比例函数y2=![]() 相交于B、C两点,交y轴于点D,连接OB,OC,OA.
相交于B、C两点,交y轴于点D,连接OB,OC,OA.

(1)求反比例函数的解析式和c的值;
(2)求△BOC的面积;
(3)直接写出当kx+b≥![]() 时x的取值范围.
时x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰直角△ABC,OC=2,抛物线y=ax2+c过A,B,C三点,D为抛物线上一点,连接BD且tan∠DBC=![]() .
.

(1)求直线BD和抛物线所表示的函数解析式.
(2)如果在抛物线上有一点E,使得S△EBC=S△ABD,求这时E点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在Rt△ABC中,AB⊥BC,点O是AC的中点,连接OB,过C点作CD⊥OB,交BO的延长线于垂足D,BC=8,sinα=![]() .
.![]()
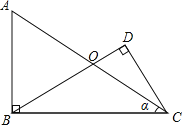
求:(1)线段OC的长;
(2)cos∠DOC的值.
查看答案和解析>>
科目: 来源: 题型:
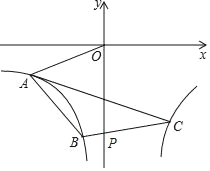
【题目】如图所示,已知双曲线y=![]() (x<0)和 y=
(x<0)和 y=![]() (x>0),直线OA与双曲线y=
(x>0),直线OA与双曲线y=![]() 交于点A,将直线OA向下平移与双曲线y=
交于点A,将直线OA向下平移与双曲线y=![]() 交于点B,与y轴交于点P,与双曲线y=
交于点B,与y轴交于点P,与双曲线y=![]() 交于点C,S△ABC=6,
交于点C,S△ABC=6,![]() ,则k=_____.
,则k=_____.
查看答案和解析>>
科目: 来源: 题型:
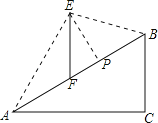
【题目】如图,在坡度i=1:![]() 的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:
的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为_____.(参考数据:![]() =1.414,
=1.414,![]() =1.732)
=1.732)
查看答案和解析>>
科目: 来源: 题型:
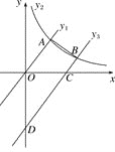
【题目】如图,直线y1=![]() x与双曲线y2=
x与双曲线y2=![]() (x>0)交于点A,将直线y1=
(x>0)交于点A,将直线y1=![]() x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
x向下平移4个单位后称该直线为y3,若y3与双曲线交于B,与x轴交于C,与y轴交于D,AO=2BC,连接AB,则以下结论错误的有( )
①点C坐标为(3,0);②k=![]() ;③S四边形OCBA=
;③S四边形OCBA=![]() ;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
;④当2<x<4时,有y1>y2>y3;⑤S四边形ABDO=2S△COD.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
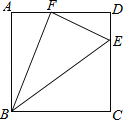
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=![]() ,则tan∠EBC的值为( )
,则tan∠EBC的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com