
科目: 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第![]() 天的成本
天的成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第
(天)之间的关系如图所示,并连续50天均以80元/件的价格出售,第![]() 天该产品的销售量
天该产品的销售量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]() .
.
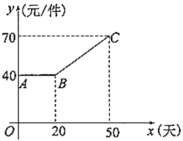
(1)第40天,该商家获得的利润是______元;
(2)设第![]() 天该商家出售该产品的利润为
天该商家出售该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在出售该产品的过程中,当天利润不低于1000元的共有多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() (
(![]() )并延长一倍得到
)并延长一倍得到![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 并延长一倍得到
并延长一倍得到![]() ,连接
,连接![]() .当
.当![]() 时,称
时,称![]() 是
是![]() 的“倍旋三角形”,
的“倍旋三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“倍旋中线”.
的“倍旋中线”.
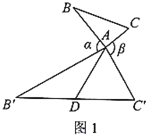
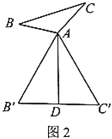
特例感知:
(1)如图1,当![]() ,
,![]() 时,则“倍旋中线”
时,则“倍旋中线”![]() 长为______;如图2,当
长为______;如图2,当![]() 为等边三角形时,“倍旋中线”
为等边三角形时,“倍旋中线”![]() 与
与![]() 的数量关系为______;
的数量关系为______;
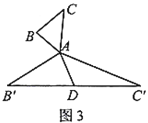
猜想论证:
(2)在图3中,当![]() 为任意三角形时,猜想“倍旋中线”
为任意三角形时,猜想“倍旋中线”![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正六边形![]() 的对称中心
的对称中心![]() 在反比例函数
在反比例函数![]() (
(![]() ,
,![]() )的图象上,边
)的图象上,边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,已知
轴上,已知![]() .
.
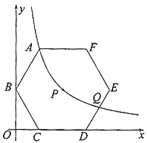
(1)点![]() 是否在该反比例函数的图象上?请说明理由;
是否在该反比例函数的图象上?请说明理由;
(2)若该反比例函数图象与![]() 交于点
交于点![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)平移正六边形![]() ,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
查看答案和解析>>
科目: 来源: 题型:
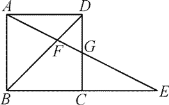
【题目】如图,在正方形ABCD中,G为CD边中点,连接AG并延长,分别交对角线BD于点F,交BC边延长线于点E.若FG=2,则AE的长度为( )
A. 6B. 8
C. 10D. 12
查看答案和解析>>
科目: 来源: 题型:
【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣![]() ,﹣1),C(
,﹣1),C(![]() ,﹣1).
,﹣1).
(1)已知点D(2,2),E(![]() ,1),F(
,1),F(![]() ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
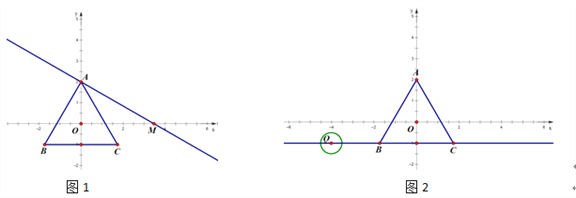
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为![]() .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
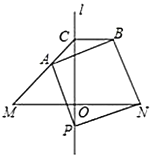
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向左平移6个单位长度,得到点
向左平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,
,![]() ,求抛物线的表达式;
,求抛物线的表达式;
(3)若抛物线![]() 的顶点在直线
的顶点在直线![]() 上移动,当抛物线与线段
上移动,当抛物线与线段![]() 有2个公共点时,求抛物线顶点横坐标
有2个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com