
科目: 来源: 题型:
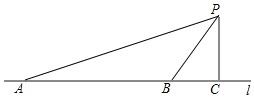
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速,如图新建的醴陵320国道(用直线l表示),进入株洲城区的AB路段设有区间测速,所有车辆限速60千米/小时(约为16.7米/秒),数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=40米,∠APC=71°,∠BPC=35°.
(1)求AB的长;
(2)若上午9时测得一汽车从点A到点B用时5.5秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目: 来源: 题型:
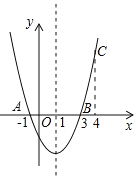
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目: 来源: 题型:
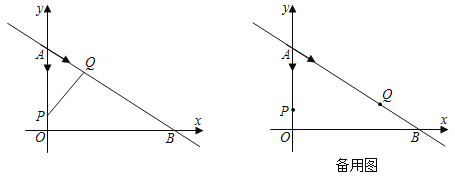
【题目】如图在平面直角坐标系xOy中,直线y=﹣![]() x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
x+6与x轴、y轴分别交于B、A两点,点P从点A开沿y轴以每秒1个单位长度的速度向点O运动,点Q从点A开始沿AB向点B运动(当P,Q两点其中一点到达终点时,另一点也随之停止运动)如果点P,Q从点A同时出发,设运动时间为t秒.
(1)如果点Q的速度为每秒![]() 个单位长度,那么当t=5时,求证:△APQ∽△ABO;
个单位长度,那么当t=5时,求证:△APQ∽△ABO;
(2)如果点Q的速度为每秒2个单位长度,那么多少秒时,△APQ的面积为16?
(3)若点H为平面内任意一点,当t=4时,以点A,P,H,Q四点为顶点的四边形是矩形,请直接写出此时点H的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】正方形ABCD与正方形DEFG按如图1放置,点A,D,G在同一条直线上,点E在CD边上,AD=3,DE=![]() ,连接AE,CG
,连接AE,CG
(1)线段AE与CC的关系为______;
(2)将正方形DEFG绕点D顺时针旋转一个锐角后,如图2,请问(1)中的结论是否仍然成立?请说明理由
(3)在正方形DEFG绕点D顺时针旋转一周的过程中,当∠AEC=90°时,请直接写出AE的长.
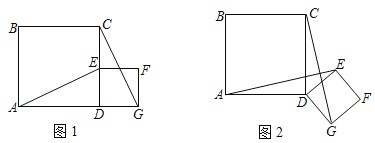
查看答案和解析>>
科目: 来源: 题型:
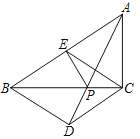
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点E是斜边AB上的一个动点,连接CE,过点B,C分别作BD∥CE,CD∥BE,BD与CD相交于点D.
(1)当CE⊥AB时,求证:四边形BECD是矩形;
(2)填空:
①当BE的长为______时,四边形BECD是菱形;
②在①的结论下,若点P是BC上一动点,连接AP,EP,则AP+EP的最小值为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】课堂上,蒋老师拿出了4张分别与有数字1,2,3,4的卡片(除数字外其他都相同),让同学们随机抽取两张,并计算这两张卡片上数字的和.
(1)请用列表或画树状图的方法列举出所有等可能的结果;
(2)求两张卡片上数字的和大于5的概率.
查看答案和解析>>
科目: 来源: 题型:
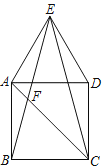
【题目】如图,在正方形ABCD的上方作等边三角形ADE,连接BE,CE.
(1)求证:△ABE≌△DCE;
(2)连接AC,设AC与BE交于点F,求∠BFC的度数.
查看答案和解析>>
科目: 来源: 题型:
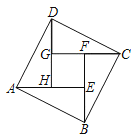
【题目】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”,通过数形结合,给出了勾股定理的详细证明如图,在“勾股弦方图”中,以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”,若正方形ABCD与正方形EFCH的面积分别为169和49,则所用细塑料棒的长度为______.
查看答案和解析>>
科目: 来源: 题型:
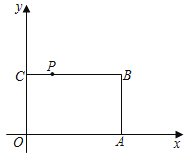
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边O在x轴上,OC在y轴上,OA=6,OC=4,PC=![]() BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转,则第2019秒时,点P的坐标为( )
A.(3![]() ,
,![]() )B.(2,﹣1)
)B.(2,﹣1)
C.(![]() ,﹣3
,﹣3![]() )D.(﹣1,2)
)D.(﹣1,2)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D是AB边上一点(不与A,B两点重合),下列条件:①∠ACD=∠B; ②∠ADC=∠ACB;③AC2=ADAB;④![]() ,能使△ABC∽△ACD的条件的个数为( )
,能使△ABC∽△ACD的条件的个数为( )
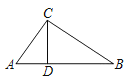
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com