
科目: 来源: 题型:
【题目】《九章算术》是中国古代数学专著在数学上有其独到的成就,不仅最早提到了分数问题,首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱又会缺16文钱,问买鸡的人数、鸡的价格各是多少?通过计算可得买鸡的人数是( )
A.6B.7C.8D.9
查看答案和解析>>
科目: 来源: 题型:
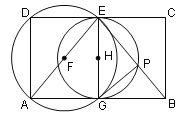
【题目】如图,矩形ABCD的面积为15,边AB比AD大2,E为CD中点,以AE为直径的⊙F交AB于G点,以EG为直径的⊙H交EB于P点,回答下列问题:
(1)求AB、AD的长;
(2)求证:PG为⊙F的切线;
(3)求PG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国福利彩票“3D单选”,每期中奖号码是从000,001,002,...,999中随机摇出1个,中奖金额为1000元,每注购买价格2元(只选1个号码,如518),回答下列问题:
(1)若某人买1注,则他中奖是_____事件(用“可能”、“不可能”或“必然”填空),中奖概率是______;
(2)若某人把所有号码各买1注,则他中奖是______事件(用“可能”、“不可能”或“必然”填空),中奖概率是_______,此时他赔_______元.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,如图1,AB是⊙O的弦,点F是![]() 的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.
(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.
(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.
(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.

查看答案和解析>>
科目: 来源: 题型:
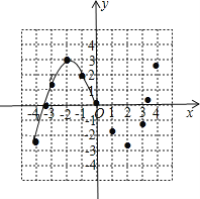
【题目】某学习小组在研究函数![]() 的图象与性质时,已列表、描点并画出了图象的一部分.
的图象与性质时,已列表、描点并画出了图象的一部分.

(1)请补全函数图象;
(2)方程![]() 实数根的个数为______;
实数根的个数为______;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车都从A地驶向B地,并以各自的速度匀速行驶![]() 甲车比乙车早行驶,甲车途中休息了
甲车比乙车早行驶,甲车途中休息了![]() 设甲车行驶时间为
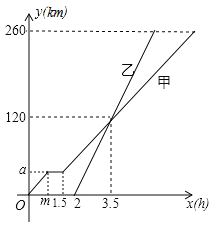
设甲车行驶时间为![]() ,下图是甲乙两车行驶的距离
,下图是甲乙两车行驶的距离![]() 与
与![]() 的函数图象,根据题中信息回答问题:
的函数图象,根据题中信息回答问题:
![]() 填空:
填空:![]() ______,
______,![]() ______;
______;
![]() 当乙车出发后,求乙车行驶路程
当乙车出发后,求乙车行驶路程![]() 与
与![]() 的函数解析式,并写出相应的x的取值范围;
的函数解析式,并写出相应的x的取值范围;
![]() 当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
查看答案和解析>>
科目: 来源: 题型:
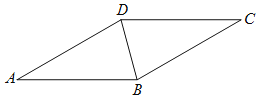
【题目】如图,BD是菱形ABCD的对角线.
(1)请用直尺和圆规作AB的垂直平分线EF,垂足为点E,交AD于点F;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,若∠CBD=75°,求∠DBF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1所示的是某超市入口的双翼闸门,如图2,当它的双翼展开时,双翼边缘的端点A与B 之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度。


查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到红球的频率稳定于0.25,求n的值.
(2)在(1)的条件下,从袋中随机摸出两个球,求两个球颜色不同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com