
科目: 来源: 题型:
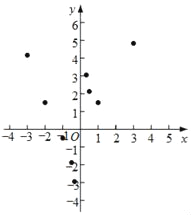
【题目】已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)从表格中读出,当自变量是﹣2时,函数值是 ;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)在画出的函数图象上标出x=2时所对应的点,并写出m= .
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且点
两点,且点![]() ,点
,点![]() 在
在![]() 轴正半轴上运动,过点
轴正半轴上运动,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() .
.
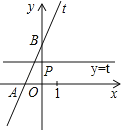
(1)求![]() 的值和点
的值和点![]() 的坐标;
的坐标;
(2)当![]() 时,直线
时,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,求反比例函数的解析式;
,求反比例函数的解析式;
(3)当![]() 时,若直线
时,若直线![]() 与直线
与直线![]() 和(2)反比例函数的图象分别交于点
和(2)反比例函数的图象分别交于点![]() ,
,![]() ,当
,当![]() 间距离大于等于2时,求
间距离大于等于2时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】豆豆妈妈用小米运动手环记录每天的运动情况,下面是她6天的数据记录(不完整):
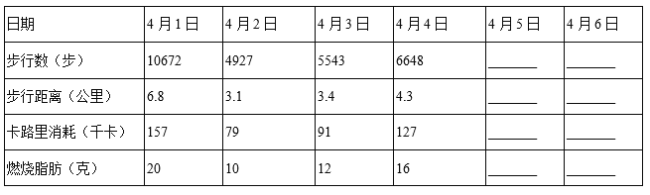
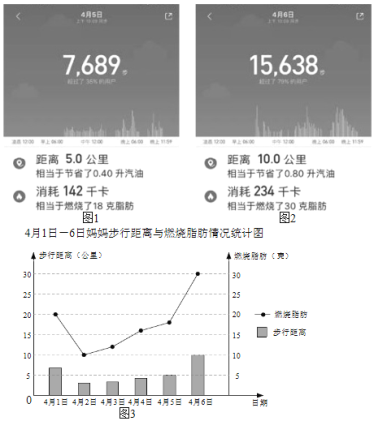
(1)4月5日,4月6日,豆豆妈妈没来得及作记录,只有手机图片,请你根据图片数据,帮她补全表格.
(2)豆豆利用自己学习的统计知识,把妈妈步行距离与燃烧脂肪情况用如下统计图表示出来,请你根据图中提供的信息写出结论: .(写一条即可)
(3)豆豆还帮妈妈分析出步行距离和卡路里消耗数近似成正比例关系,豆豆妈妈想使自己的卡路里消耗数达到250千卡,预估她一天步行距离为 公里.(直接写出结果,精确到个位)
查看答案和解析>>
科目: 来源: 题型:
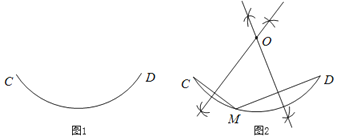
【题目】在数学课上,老师提出如下问题:尺规作图:确定图1中![]() 所在圆的圆心.
所在圆的圆心.
已知:![]() .
.
求作:![]() 所在圆的圆心
所在圆的圆心![]() .
.
曈曈的作法如下:如图2,
(1)在![]() 上任意取一点
上任意取一点![]() ,分别连接
,分别连接![]() ,
,![]() ;
;
(2)分别作弦![]() ,
,![]() 的垂直平分线,两条垂直平分线交于点
的垂直平分线,两条垂直平分线交于点![]() .点
.点![]() 就是
就是![]() 所在圆的圆心.
所在圆的圆心.
老师说:“曈曈的作法正确.”
请你回答:曈曈的作图依据是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.有下列结论;①A,B两城相距300 km;②小路的车比小带的车晚出发1 h,却早到1 h;③小路的车出发后2.5 h追上小带的车;④当小带和小路的车相距50 km时,t=![]() 或t=
或t=![]() .其中正确的结论有( )
.其中正确的结论有( )
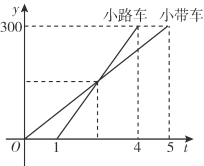
A. ①②③④B. ①②④
C. ①②D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差
查看答案和解析>>
科目: 来源: 题型:
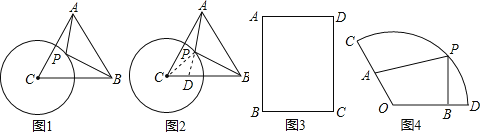
【题目】问题提出:
如图1,在等边△ABC中,AB=9,⊙C半径为3,P为圆上一动点,连结AP,BP,求AP+![]() BP的最小值
BP的最小值
(1)尝试解决:
为了解决这个问题,下面给出一种解题思路,通过构造一对相似三角形,将![]() BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
BP转化为某一条线段长,具体方法如下:(请把下面的过程填写完整)
如图2,连结CP,在CB上取点D,使CD=1,则有![]()
又∵∠PCD=∠
△ ∽△
∴![]()
∴PD=![]() BP
BP
∴AP+![]() BP=AP+PD
BP=AP+PD
∴当A,P,D三点共线时,AP+PD取到最小值
请你完成余下的思考,并直接写出答案:AP+![]() BP的最小值为 .
BP的最小值为 .
(2)自主探索:
如图3,矩形ABCD中,BC=6,AB=8,P为矩形内部一点,且PB=4,则![]() AP+PC的最小值为 .(请在图3中添加相应的辅助线)
AP+PC的最小值为 .(请在图3中添加相应的辅助线)
(3)拓展延伸:
如图4,在扇形COD中,O为圆心,∠COD=120°,OC=4.OA=2,OB=3,点P是![]() 上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
上一点,求2PA+PB的最小值,画出示意图并写出求解过程.
查看答案和解析>>
科目: 来源: 题型:
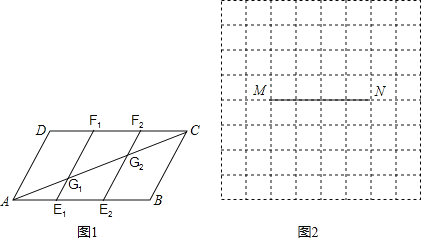
【题目】(1)如图1,在平行四边形ABCD中,点E1,E2是AB三等分点,点F1,F2是CD三等分点,E1F1,E2F2分别交AC于点G1,G2,求证:AG1=G1G2=G2C.
(2)如图2,由64个边长为1的小正方形组成的一个网格图,线段MN的两个端点在格点上,请用一把无刻度的尺子,画出线段MN三等分点P,Q.(保留作图痕迹)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
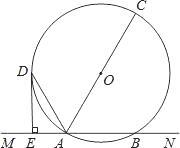
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某航天飞机在地球表面点P的正上方A处,从A处观测到地球上的最远点Q,即AQ是⊙O的切线,若∠QAP=α,地球半径为R,
求:(1)航天飞机距地球表面的最近距离AP的长;
(2)P、Q两点间的地面距离,即![]() 的长.(注:本题最后结果均用含α,R的代数式表示)
的长.(注:本题最后结果均用含α,R的代数式表示)
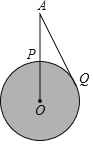
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com