
科目: 来源: 题型:
【题目】禹驰商店决定购进 A、B 两种纪念品.若购进 A 种纪念品 8 件,B 种纪念品 3 件,需 950 元;若购进 A 种纪念品 5 件,B 种纪念品 6 件,需 800 元.
(1)求购进 A、B 两种纪念品每件各需多少元?
(2)若禹驰商店决定购进这两种纪念品共 100 件,考虑市场需求和资金周转,用于购买这 100 件纪念品的资金不超过 7650 元,求禹驰商店至多购进 A 种纪念品多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
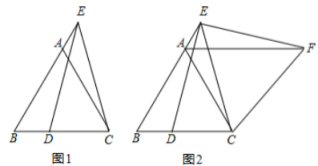
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?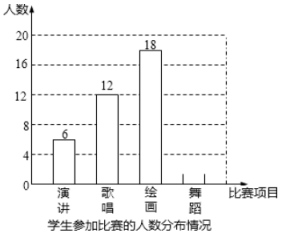
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
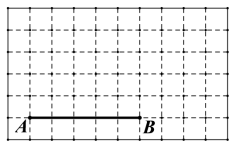
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
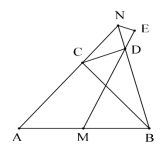
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E,DF 平分∠ADC 交边 BC 于 F,若 AD=11,EF=5,则 AB= ___.
查看答案和解析>>
科目: 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的图象如图所示:
的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交x轴于A、B两点,交y轴于点C,则平移后的解析式为 .
(2)判断△ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
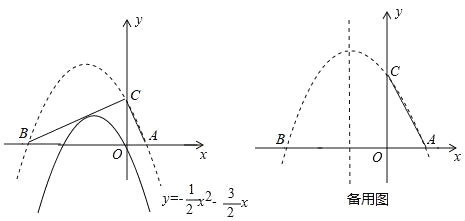
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com