
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y=![]() 的图象的一个交点为A(﹣1,n)
的图象的一个交点为A(﹣1,n)
(1)求反比例函数y=![]() 的表达式.
的表达式.
(2)若两函数图象的另一交点为B,直接写出B的坐标.
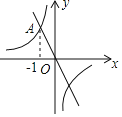
查看答案和解析>>
科目: 来源: 题型:
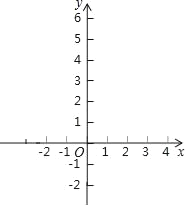
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
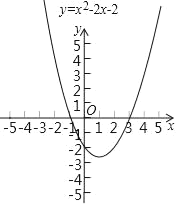
【题目】在实际问题中往往需要求得方程的近似解,这个时候,我们通常利用函数的图象来完成.如,求方程x2﹣2x﹣2=0的实数根的近似解,观察函数y=x2﹣2x﹣2的图象,发现,当自变量为2时,函数值小于0(点(2,﹣2)在x轴下方),当自变量为3时,函数值大于0(点(3,1)在x轴上方).因为抛物线y=x2﹣2x﹣2是一条连续不断的曲线,所以抛物线y=x2﹣2x﹣2在2<x<3这一段经过x轴,也就是说,当x取2、3之间的某个值时,函数值为0,即方程x2﹣2x﹣2=0在2、3之间有根.进一步,我们取2和3的平均数2.5,计算可知,对应的数值为﹣0.75,与自变量为3的函数值异号,所以这个根在2.5与3之间任意一个数作为近似解,该近似解与真实值的差都不会大于3﹣2.5=0.5.重复以上操作,随着操作次数增加,根的近似值越来越接近真实值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解与真实值的差不超过0.3,该近似解为_____
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“作一个30°角”的尺规作图过程.
已知:平面内一点A.
求作:∠A,使得∠A![]() 30°.
30°.
作法:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;
 (3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
∠DAB即为所求的角.
请回答:该尺规作图的依据是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目: 来源: 题型:
【题目】合肥某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元.设每天安排x人生产乙产品.
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | _______ | _________ | 15 |
乙 | x | x | __________ |
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润;
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)若点M是位于直线AB上方抛物线上的一动点,当![]() 的面积最大时,求此时
的面积最大时,求此时![]() 的面积S及点M的坐标.
的面积S及点M的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
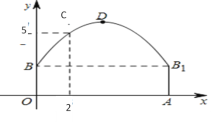
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com