
科目: 来源: 题型:
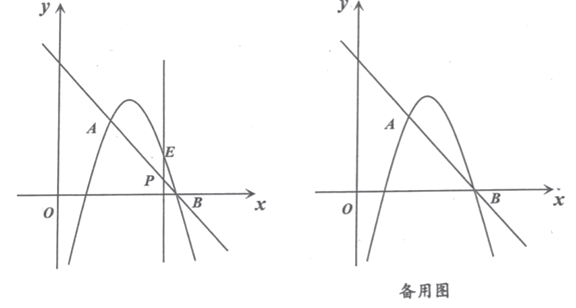
【题目】抛物线![]() 直线
直线![]() 一个交点
一个交点![]() 另一个交点
另一个交点![]() 在
在![]() 轴上,点
轴上,点![]() 是线段
是线段![]() 上异于
上异于![]() 的一个动点,过点
的一个动点,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() .
.
(1)求抛物线的解析式;
(2)是否存在这样的点![]() ,使线段
,使线段![]() 长度最大?若存在,求出最大值及此时点
长度最大?若存在,求出最大值及此时点![]() 的坐标,若不存在,说明理由;
的坐标,若不存在,说明理由;
(3)求当![]() 为直角三角形时点P的坐标.
为直角三角形时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,试求
,试求![]() 的长;
的长;
(3)如图2,点![]() 是弧
是弧![]() 的中点,连结
的中点,连结![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】某公司营销![]() 两种产品,根据市场调研,确定两条信息:
两种产品,根据市场调研,确定两条信息:
信息1:销售![]() 种产品所获利润
种产品所获利润![]() (万元)与所销售产品
(万元)与所销售产品![]() (吨)之间存在二次函数关系,如图所示
(吨)之间存在二次函数关系,如图所示
信息2:销售![]() 种产品所获利润
种产品所获利润![]() (万元)与销售产品
(万元)与销售产品![]() (吨)之间存在正比例函数关系
(吨)之间存在正比例函数关系![]()
根据以上信息,解答下列问题:
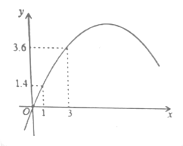
(1)求二次函数的表达式;
(2)该公司准备购进![]() 两种产品共10吨,请设计一个营销方案使销售
两种产品共10吨,请设计一个营销方案使销售![]() 两种产品获得的利润之和最大,最大利润是多少万元?
两种产品获得的利润之和最大,最大利润是多少万元?
查看答案和解析>>
科目: 来源: 题型:
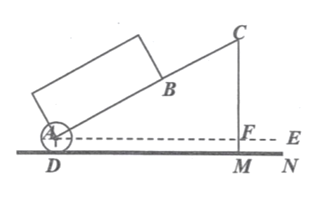
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长![]() ,拉杆最大伸长距离
,拉杆最大伸长距离![]() ,(点
,(点![]() 在同一条直线上),在箱体的底端装有一圆形滚轮
在同一条直线上),在箱体的底端装有一圆形滚轮![]() 与水平地面切于点
与水平地面切于点![]() 某一时刻,点
某一时刻,点![]() 距离水平面
距离水平面![]() ,点
,点![]() 距离水平面
距离水平面![]() .
.
(1)求圆形滚轮的半径![]() 的长;
的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点![]() 处且拉杆达到最大延伸距离时,点
处且拉杆达到最大延伸距离时,点![]() 距离水平地面
距离水平地面![]() ,求此时拉杆箱与水平面
,求此时拉杆箱与水平面![]() 所成角
所成角![]() 的大小(精确到
的大小(精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
【题目】某小区为改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为![]() ,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为
,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为![]() .
.
(1)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共![]() 吨生活垃圾,数据统计如下图(单位:吨):
吨生活垃圾,数据统计如下图(单位:吨):
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息,估计“厨房垃圾”投放正确的概率;
(2)若将三类垃圾随机投入三类垃圾箱,请用画树状图或列表格的方法求出垃圾投放正确的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表是二次函数![]() 的
的![]() 的部分对应值:
的部分对应值:
| ··· |
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
| ··· |
则对于该函数的性质的判断:
①该二次函数有最小值;
②不等式![]() 的解集是
的解集是![]() 或
或![]()
③方程![]() 的实数根分别位于
的实数根分别位于![]() 和
和![]() 之间;
之间;
④当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大;
的增大而增大;
其中正确的是:
A.①②③B.②③C.①②D.①③④
查看答案和解析>>
科目: 来源: 题型:
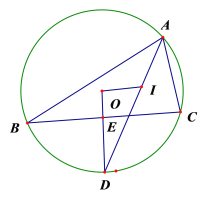
【题目】△ABC内接于⊙O,I为其内心,AI的延长线交⊙O于D,连OD交BC于E.
(1)求证: OD⊥ BC;
(2)若∠BOC=∠BIC,求∠BAC的度数;
(3)①若DE=2,BE=4,①求⊙O的半径r.
②当点A在优弧BAC上移动时,OI是否有最小值,如有请求出最小值,如没有请说明理由.
查看答案和解析>>
科目: 来源: 题型:
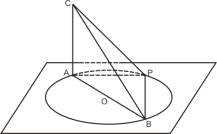
【题目】水平地面上有一个圆形水池,直径AB长为6m,长为![]() m的一旗杆AC垂直于地面(AC与地面上所有直线都垂直).
m的一旗杆AC垂直于地面(AC与地面上所有直线都垂直).
(1)若P为弧AB的中点,试说明∠BPC=90°
(2)若P弧AB为上任意一点(不与A、B重合),∠BPC=90°还成立吗,为什么?
(3)弧AB上是否存在点P使△PAB与△PAC相似,若存在求![]() 的值,不存在,说明理由.
的值,不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
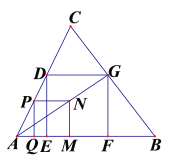
【题目】如图,正方形PQMN在△ABC内,点P在AC上,点Q、M在AB上,N在△ABC内,连接AN并延长交BC于G,过G点作GD∥AB交AC于D,过D、G分别作DE ⊥AB,GF⊥AB,垂足分别为E、F.
(1)求证:DG=GF;
(2)若AB=10,S△ABC=40,试求四边形DEFG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com