
科目: 来源: 题型:
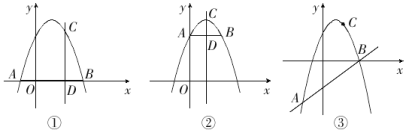
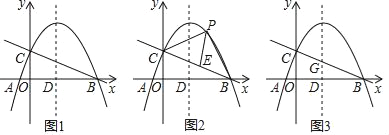
【题目】在平面直角坐标系中,直线AB与抛物线y=ax2+bx+c交于A,B(点A在点B的左侧)两点,点C是该抛物线上任意一点,过C点作平行于y轴的直线交AB于D,分别过点A,B作直线CD的垂线,垂足分别为点E,F.
特例感悟:
(1)已知:a=-2,b=4,c=6.
①如图①,当点C的横坐标为2,直线AB与x轴重合时,CD=____,|a|·AE·BF=___.
②如图②,当点C的横坐标为1,直线AB//x轴且过抛物线与y轴的交点时,CD=_____,|a|·AE·BF=_______.
③如图③,当点C的横坐标为2,直线AB的解析式为y=x-3时,CD=___,|a|·AE·BF=___.
猜想论证:
(2)由(1)中三种情况的结果,请你猜想在一般情况下CD与|a|·AE·BF之间的数量关系,并证明你的猜想.拓展应用.
(3)若a=-1,点A,B的横坐标分别为-4,2,点C在直线AB的上方的抛物线上运动(点C不与点A,B重合),在点C的运动过程中,利用(2)中的结论求出△ACB的最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=6.
,BC=6.
(1)如图1,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图2,是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点
的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需
证明).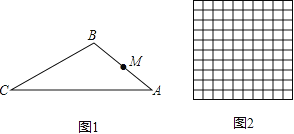
查看答案和解析>>
科目: 来源: 题型:
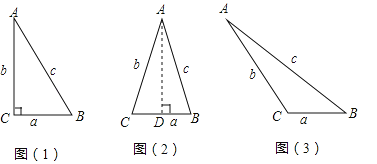
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有![]() ;若△ABC为锐角三角形时,小明猜想:
;若△ABC为锐角三角形时,小明猜想:![]() ,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,
,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .
.
∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为锐角三角形时
,∴当△ABC为锐角三角形时![]() .
.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, ![]() 与
与![]() 的大小关系.
的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
查看答案和解析>>
科目: 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目: 来源: 题型:
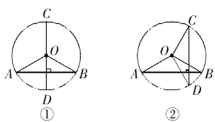
【题目】在⊙O中,AB是非直径弦,弦CD⊥AB,
(1)当CD经过圆心时(如图①),∠AOC+∠DOB=__________;
(2)当CD不经过圆心时(如图②),∠AOC+∠DOB的度数与(1)的情况相同吗?试说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农村初中2018年选拔了7名学生参加县级“综合体能”竞赛,该校2019年仍选了7名学生准备参赛,为了了解这7名学生的实力,在3月1日进行了一次与去年项目、评分方法完全一样的测试,两年成绩(单位:分)如下表:
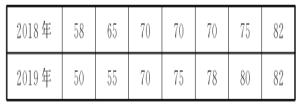
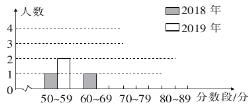
(1)请根据表中的数据补全条形统计图.
(2)分别求出两年7名学生成绩的中位数和平均数.
(3)经计算,2019年的7名学生成绩的方差s22019=136.86,那么哪年的7名学生的成绩较为整齐?请通过计算说明.
查看答案和解析>>
科目: 来源: 题型:
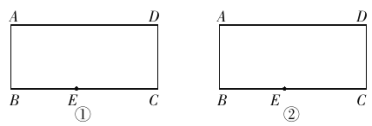
【题目】在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]
(1)在图①中,画∠BAD的平分线;
(2)在图②中,画∠BCD的平分线.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.

(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
科目: 来源: 题型:
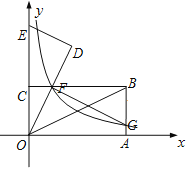
【题目】在如图平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),OA、OC分别落在x轴和y轴上,OB是矩形的对角线.将△OAB绕点O逆时针旋转,使点B落在y轴上,得到△ODE,OD与CB相交于点F,反比例函数y=![]() (x>0)的图象经过点F,交AB于点G.
(x>0)的图象经过点F,交AB于点G.
(1)求k的值和点G的坐标;
(2)连接FG,则图中是否存在与△BFG相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由;
(3)在线段OA上存在这样的点P,使得△PFG是等腰三角形.请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com